Hongzheng Chen Blog
静态程序分析 (SPA)
Mar 24th, 2020 0南京大学的李樾和谭添老师在2020年春季开设了《软件分析》课程,讲授静态程序分析(static program analysis, SPA)的相关内容。由于一直很想系统学习编译器优化及编程语言的知识,但无奈一直没有找到好的资料,国内开设相关课程的学校和老师可以说几乎没有。刚好看到谭添老师在知乎上的宣传,又恰逢疫情期间,就跟着B站的录播视频一起学了。
本文算是课程的学习笔记吧,会随着课程进度不断更新,完整的课程课件需要等两位老师放出来(已经放出来了,参见课程网站)。由于一年前我已经跟着UFMG的DCC 888学过一段静态程序分析,所以其中一些细节可能我理解了就不会再附在这。从短短几节课的感受来说,南大的课程更加适合新手入门,以Java为基础,以Soot作为静态分析工具,老师会事无巨细地讲解分析算法步骤。而UFMG的课程以C/C++为基础,以LLVM作为分析器,看上去他们的课时更加充裕,从理论到工具的使用也都有详细的讲解。
简介
编程语言(programming language, PL)的研究主要可以分为三个部分:
- 理论(theory):语言设计、类型系统、语义逻辑等
- 环境(environment):编译器、运行时系统等
- 应用(application):程序分析、程序验证、程序综合等
从上个世纪以来,语言的内核就没有怎么改变,但是程序却变得越来越大、越来越复杂,因此需要有方法确保程序的可靠性(reliability)、安全性(security)和
- Rice’s Theorem
- Any non-trivial property of the behavior of programs in a recursively enumerable language is undecidable.
这里可粗略将递归可枚举(recursively enumerable)看成是可被图灵机执行的程序(那也就是大部分程序都在这个范畴内),而非平凡(non-trivial)性质则可以认为是那些与程序运行时行为相关的性质,比如
- 是否有私有数据泄露
- 是否引用空指针
- 是否指向同一内存地址
- 某段代码是否是死代码
我们希望得到一个程序点P是否满足上述这些非平凡性质,也即给出确切的答案——是或否。但Rice定理告诉我们,这是不可能的,不存在这样完美的静态分析,能够准确判断所有非平凡性质,也即静态分析不可能既是sound又是complete的。
sound > truth > complete
- sound:过近似(overapproximate),报的错中可能有假/不是bug(假阳false positive)
- complete: underapproximate,报的错全是真的,但可能有错/bug没报出来(假阴false negative)
既然没有办法做到既sound又complete,那就只满足一个好了。大多数静态分析都妥协了complete,也即满足sound,但是不一定精确(precise)。
考虑一个类指针转换
B b = new B(); // B1
a.fld = b;
C c = new C(); // B2
a.fld = c;
// Cast
B b2 = (B) a.fld;
如果程序分析是unsound的,那么它只会分析一条路径,发现B1下来的路径没有问题,就说这个转换是safe cast;但显然这是错误的结论。只有分析是sound的,才会考虑所有路径,得出正确结论。
if (input)
x = 1;
else
x = 0;
// -> x = ?
再看上面的例子,静态分析可以有两种不同的结果:
input为真时,x=1;input为假时,x=0x=1或x=0
这两种结果都是正确的(sound),但前者精确,代价也高;后者不那么精确,计算开销小。因此静态分析想要保证soundness的同时,在分析的精度和速度上达到一个权衡。
总结来说,
抽象需要针对不同程序做不同的抽象。
比如确定一个程序中所有变量的符号,那么抽象域(abstract domain)中就需要有5个符号$+$、$-$、$0$、$\top$、$\bot$。其中,倒数第二个符号$\top$代表未知(unknown),用于处理v=e?1:-1这种变量;最后一个符号$\bot$代表未定义(undefined),用于处理v=w/0。然后就可以建立这5个符号的运算规则。
中间表示
AST & IR
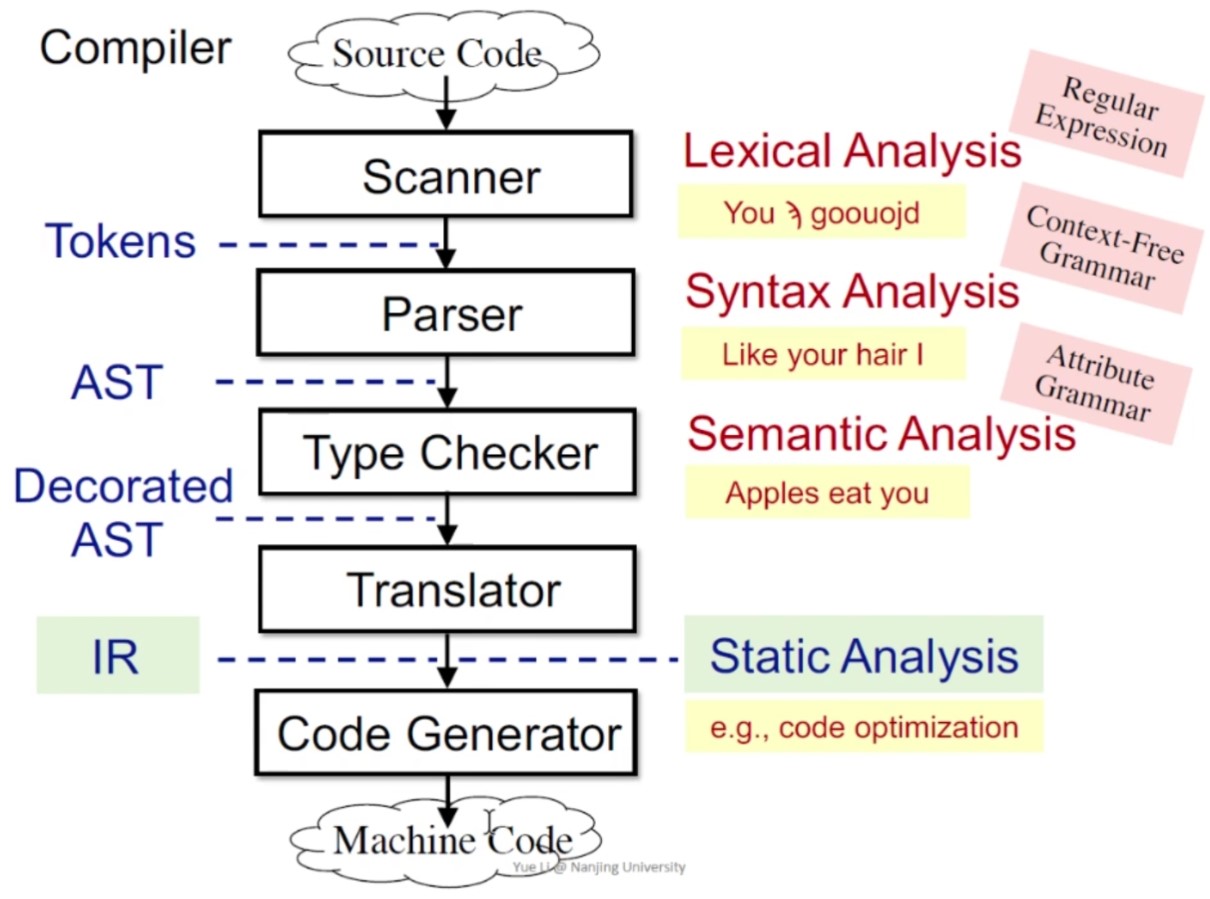
抽象语法树(abstract syntax tree, AST)和中间表示(Intermediate Representation, IR)的区别
| AST | IR |
|---|---|
| 高层贴近语言语法结构 | 低层贴近机器码 |
| 与语言相关 | 与语言无关 |
| 方便快速类型检查 | 紧凑统一 |
| 没有控制流信息 | 有控制流,静态分析基础 |
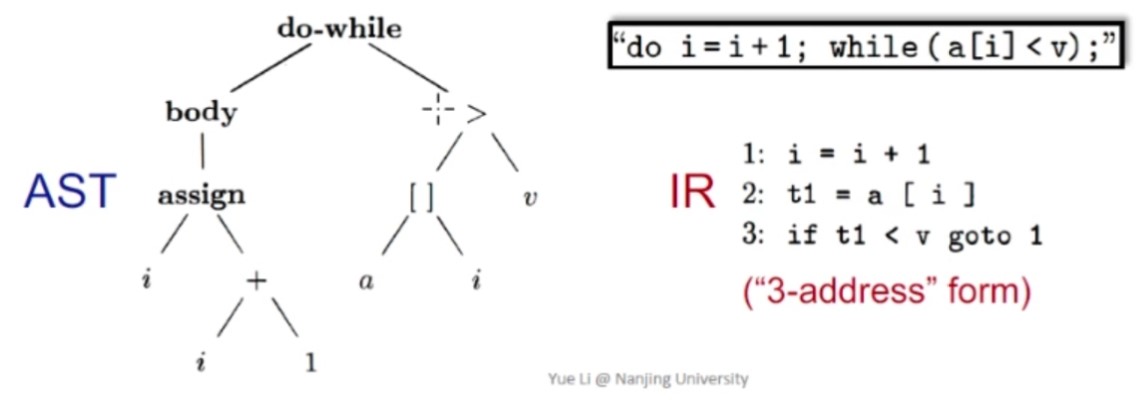
对于Java来说,静态分析的软件为Soot。
SSA
静态单赋值(static single assignment, SSA)使得3地址码(3-address code, 3AC)中的变量只有唯一一个定义,即每条语句中的变量都用不同的名字表示。
| 3AC | SSA |
|---|---|
p = a + b |
p1 = a + b |
q = p - c |
q1 = p1 - c |
p = q * d |
p2 = q1 * d |
p = e - p |
p3 = e - p2 |
q = p + q |
q2 = p3 + q1 |
当考虑分支操作时,SSA引入Phi函数。比如x0=0和x1=1汇聚,引入x2=phi(x0,x1),再进行之后的操作,确保单赋值。SSA可以让一些静态分析好操作,但是明显也带来了大量的冗余变量。
CFG
控制流图(control flow graph, CFG)的结点通常是一个基本块(basic block, BB)
基本块是最大连续的三地址码指令,满足
- 只能在第一条指令进入
- 只能在最后一条指令出去
因此创建基本块很关键的就是找到首指令(leader):
- 第一条指令是leader
- 跳转指令的目标是leader
- 指令下一条为跳转指令的为leader
在两个leader之间的则成为一个基本块。
CFG的连边需满足:
- A的末尾有一跳转指令到B
- B紧跟在A后面且A不以无条件跳转结尾
通常在最前面添加虚拟Entry结点,最后添加Exit结点。
数据流分析
基本定义
- may analysis:将所有可能是正确的结果都输出(over-approximation)
- must analysis:将所有一定正确的结果输出(under-approximation)
这两种分析方式都能使得程序是safe的,因此要看不同的情况进行分析。
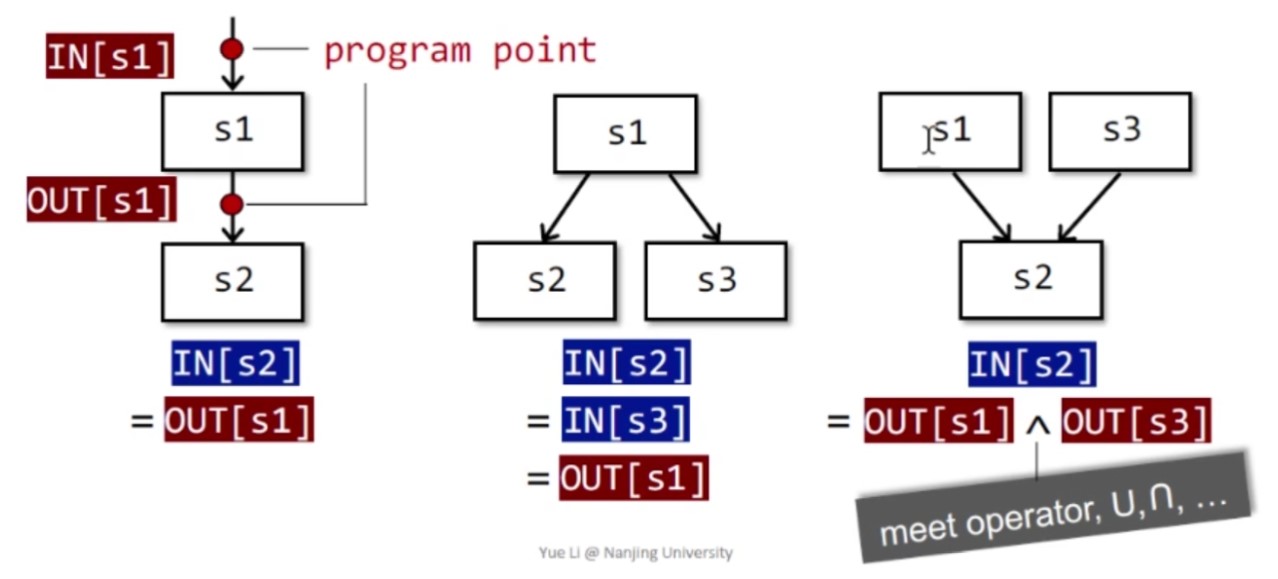
数据流分析的两条基本公式(前向)
\[\begin{cases} OUT[B] = f_B(IN[B]), f_B=f_{s_n}\circ\cdots\circ f_{s1}\\\\ IN[B] = \bigwedge_{P\text{ is a pred of B}} OUT[P] \end{cases}\]其中$s_1,\ldots,s_n$是基本块B内的$n$条指令,$\bigwedge$为meet算子。
应用举例
- 定义可达性(reaching definition)分析:如果存在一条路径使得程序点p上的定义d能够不被阻塞/不被重定义地到达q,则称定义d可达(reaches)q。
- 可用于检测可能未定义地变量,如在CFG入口为每个变量v引入冗余(dummy)定义d,如果d可以到达一个使用变量v的程序点p,则v在使用前未定义。
- 活变量(live variable)分析:如果存在一条路径使得程序点p上的变量v的值能够被使用,那么v在点p是活的,否则是死的。
- 可用于寄存器分配,比如在某点寄存器都满了,需要剔除一个,那么我们倾向于剔除死变量(今后也不会再用到的变量)。
- 从后往前分析比较好计算
- 可用表达式(available expression)分析:如果所有路径从入口到p都一定要计算表达式
x op y,且在计算x op y之后没有x和y的重定义,则称表达式x op y在点p是活的。- 即在程序点p我们可以直接将
x op y换成它最后一次计算得到的值。也可用于检测全局公共子表达式。 - 因为表达式是否可重用涉及到程序的正确性,因此需要under-approximation,报少,但一定要对,确保safe。
- 考虑下例,在点c处,
exp(16) * x表达式不应是活的,因为走左侧可能会改变其值,因此要保守估计。a = exp(16) * x / | / | x = 3 | b = exp(16) * x | \ | \ | c = exp(16) * x
- 即在程序点p我们可以直接将
总结
基本的数据流分析程序执行框架
- 输入:CFG(
kill_B和gen_B都已经为每个基本块计算好了) - 输出:对于每个基本块的IN[B]和OUT[B]
- 方法:
OUT[entry] = empty; for (each basic block B\entry) OUT[B] = ?; while (changes to any OUT occur) for (each basic block B\entry) { IN[B] = Meet_{P is a pred of B} OUT[P]; OUT[B] = gen_B \cup (IN[B] - kill_B); }
| 定义可达性 | 活变量 | 可用表达式 | |
|---|---|---|---|
| 域 | 定义集合 | 变量集合 | 表达式集合 |
| 方向 | 前向 | 后向 | 前向 |
| May/Must | May | May | Must |
| 边界 | OUT[entry]=$\varnothing$ | IN[exit]=$\varnothing$ | OUT[entry]=$\varnothing$ |
| 初始化 | OUT[B]=$\varnothing$ | IN[B]=$\varnothing$ | OUT[B]=$\cup$ |
| 转换函数 | OUT=gen$\cup$(IN-kill) | OUT=gen$\cup$(IN-kill) | OUT=gen$\cup$(IN-kill) |
| Meet | $\cup$ | $\cup$ | $\cap$ |
数据流分析-理论
如果将数据流分析中的值域设为$V$,那么可以定义
\[(OUT[n_1],OUT[n_2],\ldots,OUT[n_k])\subset(V_1\times V_2\cdots V_k)=V^k\]那么每一轮迭代相当于作用一个函数$F:V^k\mapsto V^k$,最终会到达一个不动点$X=F(X)$。
偏序
定义偏序集(poset)为$(P,\sqsubseteq)$,其中$\sqsubseteq$在$P$上定义了一个二元偏序关系,满足
- 自反性(reflexivity):$\forall x\in P,x\sqsubseteq x$
- 反对称性(antisymmetry):$\forall x,y\in P,x\sqsubseteq y\land y\sqsubseteq x\implies x=y$
- 传递性(transitivity):$\forall x,y,z\in P,x\sqsubseteq y\land y\sqsubseteq z\implies x\sqsubseteq z$
偏序意味着有些在$P$内的有些元素对是没有办法比较的。
下面的幂集是一个典型的偏序集的例子。
- 上/下界(upper/lower bound)
- 给定$(P,\sqsubseteq)$和子集$S\subset P$,若$u\in P$是$S$的上界,则$\forall x\in S,x\sqsubseteq u$;类似地,若$1\in P$是$S$的下界,则$\forall x\in S,1\sqsubseteq x$。
- 上确界(lub/join)/下确界(glb/meet)
- 所有$S$上界中最小的一个称为$S$的上确界,记为$\sqcup$;所有$S$下界中最大的一个称为$S$的下确界,记为$\sqcap$。通常,如果$S$只含两个元素${a,b}$,那么上确界可被写成$a\sqcup b$(join),下确界可被写成$a\sqcap b$(meet)。
如上例中,考虑$S$为左侧三个结点{a},{b},{a,b},则上界为{a,b}和{a,b,c},上确界为{a,b},下界和下确界都是{}。
但并不是所有偏序集都有上确界或下确界,而如果有的话一定唯一(反证法)。注意界不一定在子集$S$中。
格
- 格(lattice)
- 如果偏序集是格,则任两个元素对都有lub和glb。
故上例的幂集是一个格,join算子代表$\cup$,meet算子代表$\cap$。
- 半格(semilattice)
- 如果任两个元素对只有一侧的确界,则称其为join/meet半格。
- 完全格(complete lattice)
- 对于格的任意子集都有上下确界,那么该格称为完全格。完全格中的最大元素称为top$\top$,最小元素称为bottom$\bot$。
幂集依然是个完全格。结论:有限的格都是完全格。
- 乘积格(product lattice)
- 类似于笛卡尔积,平凑成n个维度。
不动点定理
- 单调性(monotonicity)
- 定义在格上的函数$f:L\mapsto L$是单调的,若$\forall x,y\in L,x\sqsubseteq y\implies f(x)\sqsubseteq f(y)$。
- 不动点定理(fixed-point theorem)
- 给定完全格$(L,\sqsubseteq)$,若满足(a) $f:L\mapsto L$是单调的,(b) $L$是有限的(finite),则最小不动点可以通过迭代$f(\bot),\ldots,f^k(\bot)$迭代得到,最大不动点可通过$f(\top),\ldots,f^k(\top)$迭代得到。
证明分为两个部分,存在性与最值性。存在性用经典的无穷递增与有限集矛盾,最值性用反证法。
课程大纲
- 简介
- 中间表示(IR)
- 数据流分析-应用
- 数据流分析-奠基(I)
- 数据流分析-奠基(II)
- 过程间分析
- CFL-可达性与IFDS
- Soundness和Soundiness
- 指针分析-奠基(I)
- 指针分析-奠基(II)
- 指针分析-上下文敏感
- 现代指针分析
- 安全静态分析
- Datalog分析
- 抽象解释
- 总结
作业:
- 常量传播(constant propagation, CP)
- 死代码消除(dead code elimination, DCE)
- 类层次分析(class hierarchy analysis, CHA)
- 指针分析(pointer analysis, PTA)
- 上下文敏感指针分析(context-sensitive PTA)
其他参考资料
- 熊英飞老师(北京大学),软件分析技术(Software Analysis)