Hongzheng Chen Blog
分布式系统(6) - 同步化
Jan 10th, 2020 0瞬时同步
瞬时同步的主要问题
- 瞬时-> 不持久 -> 要求双方都在线,不然通信无法进行,会丢失
- 同步:由于等待带来了很大的性能浪费,无法通过并发来实现性能的提升
- 可扩展性不佳,对系统中节点不宕机的假设不现实,大规模系统中的高并发无法实现
解决方案:
- 使用消息中间件实现消息的持久化存储
- 实现异步通信,利用并发提升系统性能
时钟同步算法
引入多CPU,每个CPU都有自己的时钟,则会产生时钟偏移(clock skew)。
- 外同步:外部时间源(UTC)
- 内同步:机器内部时钟信号
假设每台机器都有一个每秒产生\(H\)次中断的计时器。当计时器产生中断时,中断处理程序将软件时钟加1,软件时钟记录从过去某一约定时间开始的滴答/中断数,记为\(C\)。当UTC时间为\(t\)时,\(P\)上时钟值为\(C_p(t)\)。最理想情况是对于所有的\(p\)和\(t\)都有\(C_p(t)=t\),即\(\mathrm{d}C/\mathrm{d}t\)理想值为1。
若存在某一常数\(\rho\)使得
\[1-\rho\leq\frac{\mathrm{d} C}{\mathrm{d} t}\leq 1+\rho\]则可以说计时器在规定范围内工作,\(\rho\)由厂商规定,称为最大偏移率(maximum drift rate)。
若两个时钟以相反方向偏离UTC,则在其同步后的\(\Delta t\)绝对时间内,最大可能偏差可能达到\(\delta=2\rho\Delta t\)。
网络时间协议
让客户A与时间服务器B联系
| B | 接收\(T_2\) | 响应\(T_3\) | ||
| A | 请求\(T_1\) | 到达\(T_4\) |
进而A可以计算出与B的时间偏差(B的当前时间-A的当前时间)
\[\theta=\left(T_3+\frac{(T_2-T_1)+(T_4-T_3)}{2}\right)-T_4=\frac{(T_2-T_1)+(T_3-T_4)}{2}\]但时间是不能往后退的,只能逐步来调整。假设计时器每秒产生100个中断,正常情况每个中断添加10毫秒,通过每个中断只添加9毫秒可以将时间往后调,每个中断添加11毫秒则往前调。
网络时间协议(Network Time Protocol, NTP)在服务器之间创建了两条连接,延迟计算如下
\[\delta=\frac{(T_2-T_1)+(T_4-T_3)}{2}\]可以将每个\((\theta,\delta)\)对缓存起来,最后以\(\delta\)的最小值作为两个服务器之间的延时,从而相应的\(\delta\)是最可靠的偏差。
Berkeley算法
在NTP中,时间服务器是被动的;而Berkeley UNIX则采用主动的时间服务器(时钟守护程序),计算时间均值,并告诉其他机器应该如何根据当前时间进行调整。
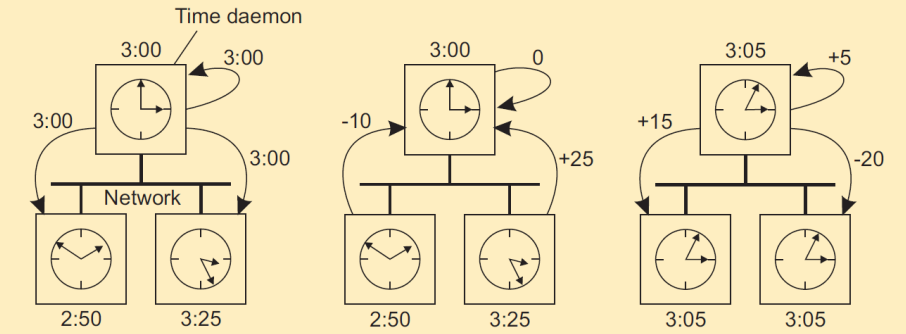
(a)时间守护程序询问其他机器时钟值,(b)其他机器做出应答,(c)时间守护程序告诉每台机器应该如何调整时钟。
注意在Berkeley算法中并没有采用UTC全局时钟。
无线网络中的时钟同步
参考广播同步化(Reference Broadcast Synchronization, RBS)同样没有假设具有精确时间的结点,不为所有结点提供UTC时间,而只是在内部实现时钟同步化。
前面的协议都是遵循双向协议(发送器和接收器实现同步),而RBS只是使接收器同步化,发送器则位于该循环外。
当一个结点广播一个参考消息\(m\)时,每个结点p只是记录它收到\(m\)的时间\(T_{p,m}\),这里的时间是从\(p\)的本地时钟读取的。忽略时钟偏差,两个结点p,q就可以交换各自的传送时间。
\[deviation[p,q]=\frac{\sum_{k=1}^{M}(T_{p,k}-T_{q,k})}{M}\]其中\(M\)为发送的参考消息总数。(实际上就是蒙特卡洛) 改进的算法则用标准线性回归
\[deviation[p,q](t)=\alpha t+\beta\]来计算偏差。
逻辑时钟
前面都假设时间同步化与实际时间相关,但实际上在很多应用中,只要所有机器具有相同时间就足够了,这个时间不一定要与实际时间相同。
Lamport逻辑时钟
定义“先发生”(happens-before)的关系\(a\to b\),如果\(x\to y\)不为真,\(y\to x\)也不为真,则这两个事件称为并发的。这样就可以给每一个事件\(a\),分配一个所有进程都认可的时间值\(C(a)\)
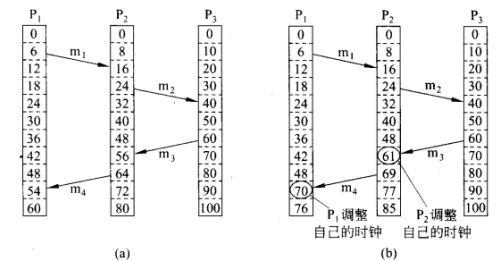
由于“先发生”关系,故时钟一定不会往后流,因此当从P3发消息回P2和P1时会促使它们的时钟至少往前进1格。
具体实施则每个时钟\(P_i\)维护一个局部计数器\(C_i\),按照以下步骤更新:
- 在执行一个事件之前(网络上发消息,传消息给应用程序或其他内部事件),\(P_i\)执行\(C_i\gets C_i+1\)
- 进程\(P_i\)发消息给\(P_j\)时,把\(m\)的时间戳\(ts(m)\)设为\(C_i\)
- 接收消息\(m\)时,进程 \(P_j\) 调整自己的局部计数器为 \(C_j\gets \max\{C_j,ts(m)\}\),然后执行第一步,将消息传送给应用程序
在具体实施中则采用中间件调整本地时钟
全序多播
全序多播(totally ordered multicast)即一次将所有的消息以同样的顺序传送给每个接收者的多播操作。
- 进程收到一个消息后,将其放入一个本地队列中,并根据其时间戳进行排序
- 接收者向其他所有进程广播确认
- 只有队列中一个消息处于队列头,且被其他所有进程确认时,进程才可以将其传送给运行中的应用程序
因为每个进程都有相同的队列,所以在任何地方,所有消息都以同样的顺序交付。
互斥访问及临界区访问
利用Lamport逻辑时钟解决
- 前提:在同一个时刻至多允许一个进程执行一个“关键区”代码片段
- 实现:与全序多播类似,所有进程建立单独的队列,以相同的顺序发送消息,只要“ENTER”消息的接受 在全体进程的接受顺序上达成一致,就可以了
- 其实和全序多播一样,只要把进入临界区理解成处理某进程的ENTER消息就好,通过全序多播就能够 得到这个消息的处理顺序一致且互斥
向量时钟
Lamport时间戳不能捕获因果关系(causality),因果关系要通过向量时钟来捕获。
如果对于事件 \(b\),有 \(VC(a)<VC(b)\) 那么认为事件 \(a\) 为因, \(b\) 为果。
向量时钟通过令每个进程 \(P_i\) 维护一个向量 \(VC_i\) 来完成:
- \(VC_i[i]\) 是进程 \(P_i\) 的逻辑时钟,也即在 \(P_i\) 上发生的事件数量
- 若 \(VC_i[j]=k\) 则 \(P_i\) 知道有 \(k\) 个事件在 \(P_j\) 上完成( \(i \neq j\) )
实际上就是对于每一个进程i维护一个所有进程状况的数组/向量,每一个元素为一个Lamport逻辑时钟。
具体更新步骤:
- 执行一个事件之前, \(P_i\) 执行 \(VC_i[i]\gets VC_i[i] + 1\) (注意无论是接收还是发送消息都需先执行这一步)
- 当进程 \(P_i\) 发送消息 \(m\) 给 \(P_j\) 时,在执行完前面步骤后,将 \(m\) 的时间戳 \(ts(m) \gets VC_i\)
- 接收消息 \(m\) 时,进程 \(P_j\) 通过为每个 \(k\) 设置 \(VC_j[k]\gets\max\{VC_j[k],ts(m)[k]\}\) 来调整自己的向量
强制因果有序通信
称 \(b\) 因果依赖于 \(a\) 若消息时间戳 \(ts(a) < ts(b)\)(严格不等式),且
- 对于所有 \(k\) , \(ts(a)[k] < ts(b)[k]\)
- 存在至少一个 \(k'\) , 使得 \(ts(a)[k'] < ts(b)[k']\)
因果有序多播(causally-ordered)比全序多播更弱,当两个消息互相没有任何关系时,则不用关心以何种顺序传送给应用程序。 并且假设只在发送和接收消息时才调整时钟。
调整:仅当 \(P_i\) 发送消息时才增加 \(VC_i\) , \(P_j\) 接收到消息才调整 \(VC_j\)
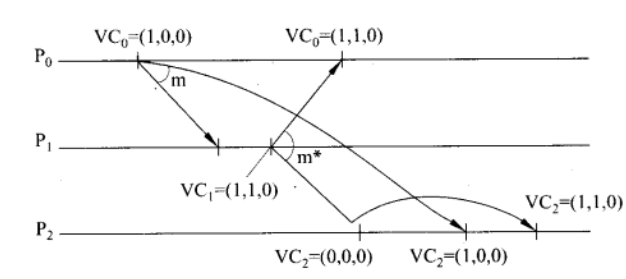
现在假设进程 \(P_j\) 从进程 \(P_i\) 接收到一个向量时间戳为 \(ts(m)\) 的消息 \(m\) ,则该消息传送到应用层将会被延时,直到满足以下条件:
- \[ts(m)[i]=VC_j[i] + 1\]
- \[ts(m)[k]\leq VC_j[k],k \neq i\]
第一个条件表示消息 \(m\) 是进程 \(P_j\) 希望从 \(P_i\) 接收的下一条消息,而第二个条件则表示当进程 \(P_i\) 接收发送消息 \(m\) 时, \(P_j\) 已经收到所有来自进程 \(P_i\) 的消息。
互斥
基于令牌的算法、基于许可的算法
集中式算法
选举一个进程作为协作者(如运行在最大网络地址号机器上的进程),然后访问共享资源的方式即
- P1请求协作者访问共享资源
- P2请求协作者访问共享资源时,协作者不允许,将其放入队列中
- P1释放资源时通知协作者
- 协作者对P2作出回应
缺点:单点失效
非集中式算法
利用分布式哈希表(DHT),假定每种资源有 \(N\) 个副本,每一个副本都有自己的协作者用于控制访问。进程只需获得 \(m>N/2\) 个协作者的大多数投票就可以访问资源。
分布式算法
Ricart和Agrawala(1981)对Lamport(1978)的算法进行了改进,要求系统中所有事件都完全排序。
- 若接收者没有访问资源,也不想访问它,就向发送者发送OK
- 若接收者已获得对资源的访问,则它不作应答,而是将该请求放入请求队列中
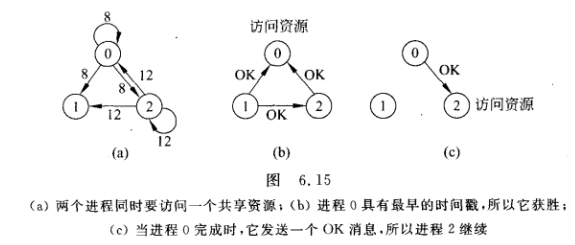
- 如果接收者想访问资源但尚未访问时,它将收到的消息的时间戳与包含在它发送给其他进程的消息中的时间戳进行比较。时间戳最早的那个进程获胜。如果收到的消息的时间戳比较早,则接收者向发送者发回OK。如果它自己的消息的时间戳比较早,则接收者将收到的请求放入队列中,且不发送任何消息。
令牌环算法
- 环初始化时,进程0得到一个令牌(token)
- 令牌绕着环运行,用点对点发送消息的方式将令牌从进程k传到k+1(以环大小为模)
- 进程从它邻近的进程得到令牌后,检查自己是否需要访问资源。如果要则继续完成其工作,然后释放资源;否则继续传递。
- 在该进程完成后,沿环继续传递令牌。
如果令牌丢失了,则需要重新生成令牌,但很难确定是丢失了还是仍在使用。
总结
| 算法 | 每次进/出需要消息数 | 进入前延迟(按消息数) | 问题 |
| 集中式 | 3 | 2 | 协作者崩溃 |
| 非集中式 | 3mk | 2m | 会发生饥饿,效率低 |
| 分布式 | 2(n-1) | 2(n-1) | 任何进程崩溃 |
| 令牌环 | \(1\thicksim\infty\) | \(0\thicksim n-1\) | 令牌丢失,进程崩溃 |
选举算法
某些算法需要一些进程作为协作者,问题是如何动态选择这个特殊的进程。在很多系统中,协作者手动选取,这会导致集中化的单点失效问题。
基本假设:
- 所有进程都有唯一ID
- 所有进程都知道其他进程ID,但不知道进程运行还是停止
- 选举算法找到具有最大ID运行的进程
Bully算法
当任何进程发现协作者不再响应请求时,就发起一次选举。进程P按如下过程主持一次选举:
- P向所有编号比它大的进程发送一个ELECTION消息
- 如果无人响应,P获胜成为协作者
- 如果有编号比它大的进程响应,则响应者接管选举工作。P的工作完成。
直到最大编号可响应进程,向所有进程发送COORDINATOR消息,成为新的协作者。
环算法
- 任何进程都可以启动一次选举,该进程将选举消息传递给后继者,如果后继者崩溃,则消息依次传递
- 在每一步传输中发送者将自己的进程号加到该消息的列表中,使自己成为协作者候选人
- 消息返回到此次选举的进程,消息类型转为COORDINATOR消息,再次绕环通知所有进程谁是协作者及新环中成员有谁
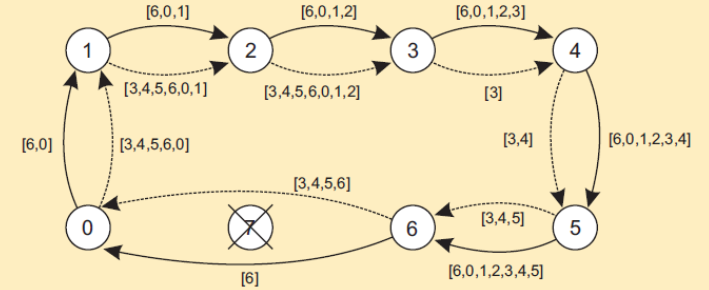
无线网络中的选举算法
传统选举算法假设消息传送是可靠的,网络拓扑结构也是不改变的,但在无线网络中就不能这样。
下图展现了选举过程,其中每个结点为资源容量,越大越好(会成为协调者)。
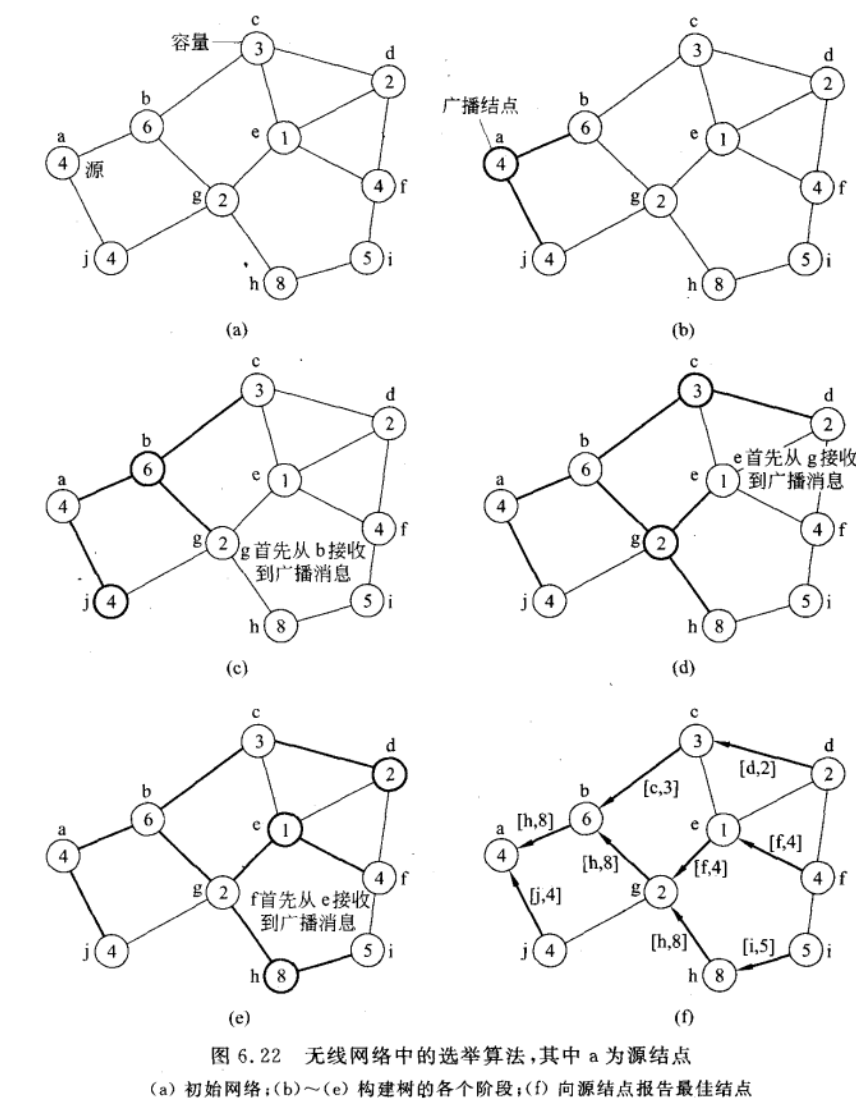
从节点a开始发起选举,然后每个结点向父节点报告具有最佳容量的结点,最后再由a将协调者信息广播出去。