静态程序分析

Feb 15th, 2019 0

本课程采用巴西米纳斯联邦大学(Universidade Federal de Minas Gerais, UFMG)的Static Program Analysis - DCC888讲义。至于为什么选择这么一所名不见经传的大学的课程，一部分原因纯属偶然搜到，其他原因则有

非常清晰易懂，幻灯片上图文并茂，力求将概念解释清楚
没有繁琐的全套编译器的介绍，而着重讲解中间优化器的部分
基本的优化技术都有涉及，广度是足够的
以llvm作为实验基石，同时也附带抽象代数、函数式编程等内容，是一门理论与实践相结合又十分前沿的课程
附带讲讲编译器的历史，同时都附有参考文献

1. 简介

课程简介

软件工程师需要抽象，硬件工程师需要效率，编译器弥合两者

主要目的：如何自动变换程序，且保持原来的语义但是性能更高
次要目的：理解那些离开机器帮助就无法实施的编译技术
程序优化+找bug

There is no Silver Bullet 不可能造出完美优化编译器(perfect optimizing compiler)

The Full-Employment Theorem 如果A是某一面向图灵完备语言的优化编译器，那么一定可以造出一个比A更好的编译器

Compiler is a microcosm of CS

Algorithms: graphs
AI: ML
Automata: DFA
Algebra: lattices, fixed point theory, Galois connections, type systems
Architecture: pipeline, memory hierarchy, ISA
Optimization: scheduling

静态与动态分析

动态分析
- profiling
- test generation
- emulation
- instrumentation
静态分析（本课程重点）
- dataflow: liveness, reaching definitions, constant propagation
- constraint-based: control flow, pointer analysis
- type

历史

1950s, Fortran，第一个被编译器优化的编程语言
Frances E. Allen, John Cocke提出了很多优化概念，大多在IBM Labs实现
Gary Kildall，现代代码分析优化之父，dataflow monotone framework
Cousot, 一篇非常有影响力的论文，Abstract Interpretation
Gregory Chaitin，寄存器分配，图染色
Cytron，静态单一表示(SSA)
Olin Shivers，控制流分析
Benjamin Pierce，Types and Programming Languages，非常有影响力的书籍

当前的挑战

并行化
动态语言
正确性
安全

未来会导向两条道路，Hall, Padua e Pingali, Compiler Research: The Next Fifty Years, Communications of the ACM, 2009

自动并行化
自动bug检测

2. 控制流图

控制流图(control flow graph, CFG)是一个有向图

结点为基本块(basic block, BB)
如果程序执行能从块B1到块B2，那么B1与B2之间连边

LLVM (Low-Level Virtual Machine)

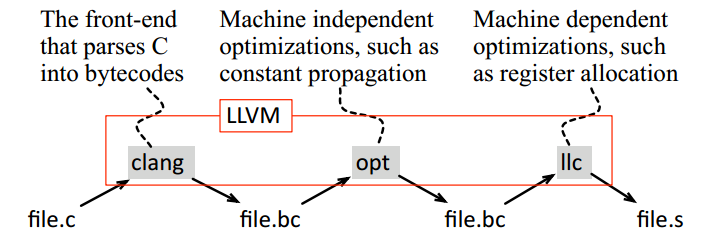
整体编译流程

LLVM is a framework with lots of tools to compile and optimize code

LLVM flow

$> clang -c -emit-llvm identity.c -o identity.bc
$> opt -mem2reg identity.bc -o identity.opt.bc
$> llc -march=x86 identity.opt.bc -o identity.x86

简介

LLVM用一系列字节码表示程序，并不针对特定机器

字节码具有可移植性(portable)，可以被解释(interpretable)
lli以JIT方式解释执行

用LLVM可视化CFG

opt -view-cfg identity.bc

优化级别分为-O0(默认)、-O1、-O2、-O3，下面指令可看是每一级有哪些优化

llvm-as < /dev/null | opt -O3 -disable-output -debug-pass=Arguments

每一个编译分析或变换称为一趟(pass)

机器无关优化：opt
机器相关优化：llc

LLVM的层次结构：Module > Function > Block > Instruction > Operand
一个例子

for(Function::iterator bb = F.begin(), e = F.end(); bb != e; ++bb) {
    for(BasicBlock::iterator i = bb->begin(), e = bb->end(); i != e; ++i) {
        if(opCounter.find(i->getOpcodeName()) == opCounter.end()) {
            opCounter[i->getOpcodeName()] = 1;
        } else {
            opCounter[i->getOpcodeName()] += 1;
        }
    }
}

基本块(Basic block)：最大连续指令满足
- 控制流只能从第一条指令(leader)进入BB
- 除了BB的最后一条指令，控制流不会停止、分支、离开BB 也即，对于每个基本块，包含leader以及到下一leader之间的部分

LLVM IR

RISC指令级，有指令码(opcodes)
有类型表示
- %0 = load i32* % X, align 4
静态单赋值(Static Single Assignment, SSA)格式
显性表示控制流

局部优化

DAG-based
Peephole
Local register allocation

DAG优化

基本块内用有向无环图(DAG)表示

每一个输入值（在第一次使用前没有定义/赋值）都有一个结点
BB内每条指令对应一个结点
如果指令S用了指令S1，…，Sn定义的变量，则Si到S都有边
BB内定义但没使用的称为输出值

DAG的表示

对于每个输入值vi
- 创建结点vi
- 标注这个结点为in
对于每个声明v=f(v1,…,vn)
- 创建结点v
- 建边(v,vi)
- 标记结点为f

局部公共子表达式(local common subexpression)：注意需要整条指令相同才算公共

若DAG已包含结点v’标记为f，且孩子按照v1,…,vn顺序，则令v’为v的别名(alias)
将每个结点赋一个签名(signature)(lb,v1,…vn)，其中lb为标签
- 可以将此签名作为哈希函数的键值(key)
- 哈希函数的值称为变量的值数字(value number)
- 因此可以在每次建结点前找哈希表，如果存在结点则直接返回引用

死代码消除(dead code elimination)

如果结点没有后代(descendant)，即为根结点(root)
该结点没有被标记为输出结点

代数恒等式

算术等式：x+0=x
消减常数：x^2=x*x
常量折叠：在编译时将值计算出来

窥孔优化(peephole)

优化器每次只分析一个小窗口里面的连续几条指令
窗口滑动过整个代码段，一旦某个窗口的模式被识别即进行优化

Redundant loads and stores

load r0, m
store m, r0

Branch transformations

if debug == 1 goto L1
goto L2
L1: …
L2: …

// optimization
if debug != 1 goto L2
L1: …
L2: …

Jumps to jumps

goto L1
...
L1: goto L2

// optimization
goto L2

局部寄存器分配

寄存器十分少量，但是运算速度极快
Belady Algorithm [1]，有点LRU的感觉，溢出(spill)则驱除(evict)入内存
- 注意这个算法是最优的（寄存器大小一样条件下；若不同大小则NP完全）
注意具体实施时就在指令前后加load store指令

参考文献

Belady, A Study of Replacement algorithms for a Virtual Storage Computer, IBM Systems Journal, 1966
Lattner, C. (UIUC), and Adve, V., LLVM: A CompilaLon Framework for Lifelong Program Analysis & TransformaLon, CGO, 2004

3. 数据流分析

存在一个通用的算法能够从程序中提取信息，即所谓的数据流分析。

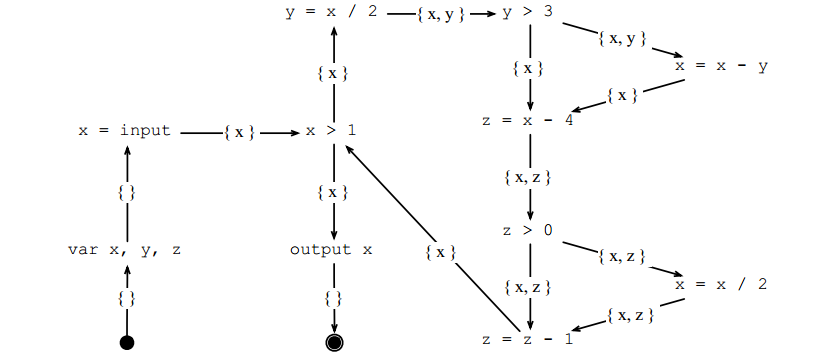
活性(Liveness)

假设有无限供应的寄存器，那么在程序点(program point)p，变量v应该在寄存器中存活(alive)当

有一条路径P从p到另一个也使用了v的程序点pu
路径P不经过任何v的定义点

变量在程序点p前即刻存活(alive immediately)，当且仅当

它在p之后即刻存活
它没有在p被重定义

或

它在p点被使用

实际上活性就是指变量存放在寄存器内的最小时间区段

对于赋值表达式p:v=E，其活性数据流方程为

$IN(p)=(OUT(p)\ {v}\cup vars(E)\ OUT(p)=\bigcup IN(p_s),p_s\in succ(p)$

活性的信息流向是从后往前流。

算法：

初始化所有IN和OUT为空集
计算所有方程
如果有任何IN或OUT的集合改变，那就重新执行上一步，直到没有方程改变为止

liveness

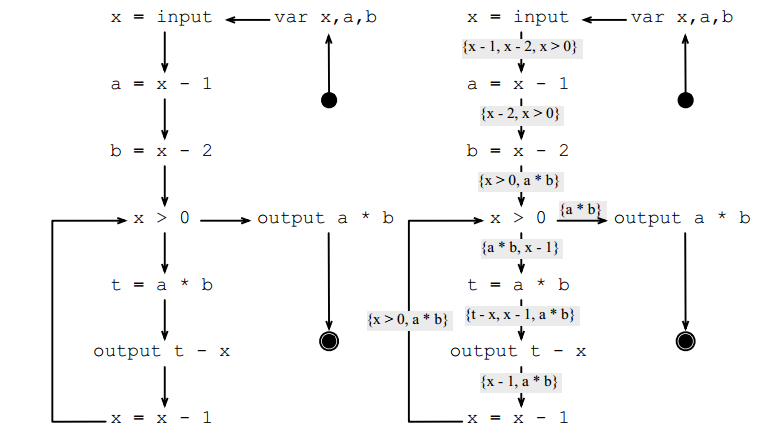
可用表达式(Available expressions)

若某条表达式的当前值之前已经被计算出来，那就称其为可用表达式，可以直接用之前的变量替换掉

表达式E在程序点p之后即刻可用(available immediately)，当且仅当

它在p前即刻可用
没有E的变量在p点重定义

或

它在p使用了
没有E的变量在p点重定义

对于赋值表达式p:v=E，其可用表达式数据流方程为

\[IN(p)=\cap OUT(p_s),p_s\in pred(p)\\ OUT(p)=(IN(p)\cup\{E\}\ \{Expr(v)\}\]

可用表达式的信息是从前往后流。

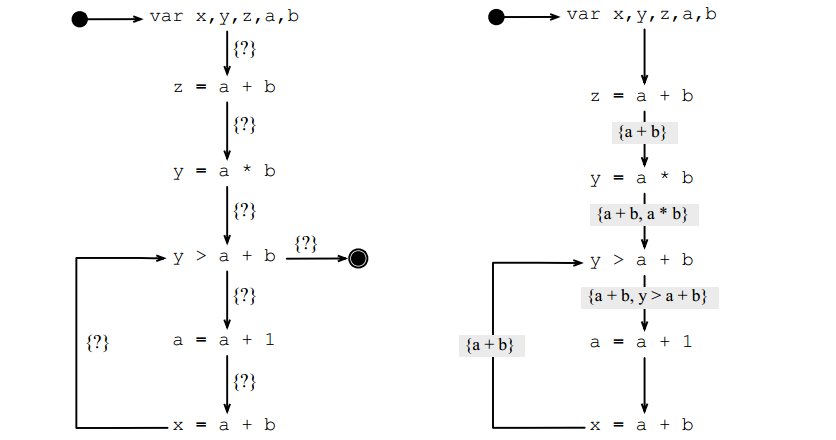
availability

很忙表达式(Very busy expressions)

一个表达式在程序点非常忙当它无论沿哪条路径从那个点到终止点都会被计算。

类似可得数据流方程，从后往前流

very-busy-expressions

进而可以将很忙表达式的计算前移，如上例的a*b可移动到循环前，这是performance safe的。

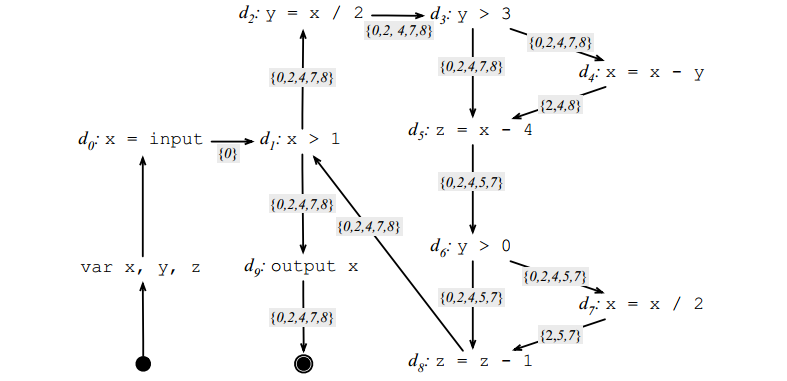
可达性定义(Reaching definitions)

变量v在程序点p的定义可到达程序点p’，若有一条路径从p到p’，且这条路径不经过任何v的重定义

同样从前往后流

reaching-definitions

总结：单调框架(The Monotone Framework)

dataflow-framework

A may analysis keeps tracks of facts that may happen during the execution of the program. - A definition may reach a certain point.
A must analysis tracks facts that will – for sure – happen during the execution of the program. - This expression will be used after certain program point.

抽象解释(abstract interpretation)

转移函数(transfer functions)提供了一种新的解释程序的方法。
可以建造一台机器遍历程序，抓取给定指令，并且应用转移函数，直到这些转移函数不再改变，即抽象解释。
合并函数(merging functions)（转移函数的组合）保证了抽象解释会停止

参考文献

数据流分析是最早的编译优化技术之一
Frances Allen因数据流分析获得了2007年的图灵奖

Allen, F. E., Program Optimizations, Annual Review in Automatic Programming, 1969 2. Allen, F. E., Control Flow Analysis, ACM Sigplan Notices, 1970
Kam, J. B. and J. D. Ullman, Monotone Data Flow Analysis Frameworks, Actal Informatica, 1977
Kildall, G., A Unified Approach to Global Program Optimizations, ACM Symposium on Principles of Programming Langua

4. 工作表算法

求解数据流分析中的限制系统(constraint systems)。

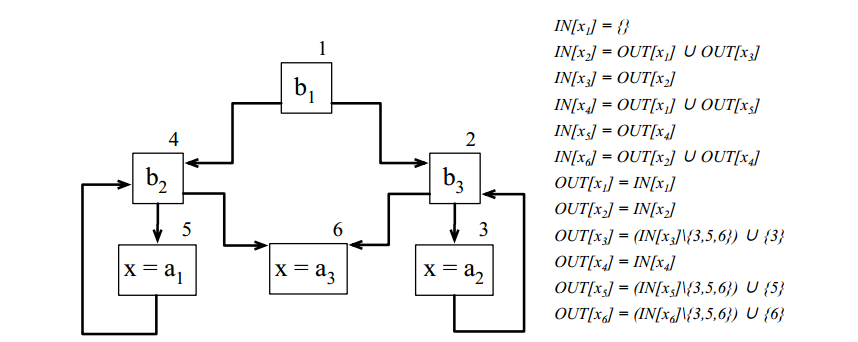
用Prolog解限制方程

if b1
  then
    while b2 do x = a1
  else
    while b3 do x = a2
x = a3

可达性定义 prolog example

solution([X1_IN, X2_IN, X3_IN, X4_IN, X5_IN, X6_IN,
          X1_OUT, X2_OUT, X3_OUT, X4_OUT, X5_OUT, X6_OUT]) :-
    X1_IN = [],
    union(X1_OUT, X3_OUT, X2_IN),
    X3_IN = X2_OUT,
    union(X1_OUT, X5_OUT, X4_IN),
    X5_IN = X4_OUT,
    union(X2_OUT, X4_OUT, X6_IN),
    X1_OUT = X1_IN,
    X2_OUT = X2_IN,
    diff(X3_IN, [3, 5, 6], XA), union(XA, [3], X3_OUT),
    X4_OUT = X4_IN,
    diff(X5_IN, [3, 5, 6], XB), union(XB, [5], X5_OUT),
    diff(X6_IN, [3, 5, 6], XC), union(XC, [6], X6_OUT),
    !.

union([], S, S).
union([H|T], S, [H|SU]) :- union(T, S, SU).
diff([], _, []).
diff([H|T], S, SD) :- member(H, S), diff(T, S, SD).
diff([H|T], S, [H|SD]) :- \+member(H, S), diff(T, S, SD).

在solution前面用,加限制length(X5_OUT,1)避免无穷序列

false negative：如果实际可以而理论分析不行，则为错误(wrong)
false positive：如果理论分析可以而实际不行，则是不精确的(imprecise)，而不是错误

迭代工作表求解器(iterative worklist solvers)

混乱(chaotic)迭代

将所有限制放入包中，随机打乱
从中拿出限制C，求解
如果没有东西改变
- 若还有限制在包中，则跳回2
- 否则完成
否则跳回1

涉及到不动点理论。尽管没有规定求解顺序，但是最终始终会到达不动点。

找到一种特定的顺序，可以使求解速度加快。

强连通图缩点拓扑序，可保证之后求解的不影响之前的。

用位向量可以压缩存储。

参考文献

Kildall为第一个worklist算法的工作
Horwitz第一个用强连通分量方法解数据流问题

Kildall, G., A Unified Approach to Global Program Optimization, POPL, 1973
Hecht, M. S., Flow Analysis of Computer Programs, North Holland, 1977
Horwitz, S. Demers, A. and Teitelbaum, T., An efficient general iterative algorithm for dataflow analysis, Acta Informatica 24, 1987

5. 格论

格论(Lattices)尝试回答以下两个问题

如何知道数据流分析的算法会停止
该算法的解的精确性有多高

简介

一个完整的格$L=(S,\leq,\lor,\land,\bot,\top)$由以下几个元素组成

集合$S$
集合$S$上的偏序$\leq$
最小(least)元素$\bot$
最大(greatest)元素$\top$
组合(join)算子$\lor$
相交(meet)算子$\land$

注意最大最小元素唯一

算子性质：恒等律(idempotent)、交换律、结合律

Join有零元$\top\lor x=\top$，幺元$\bot\lor x=x,\forall x\in S$
Meet有零元$\bot\land x=\bot$，幺元$\top\land x=x,\forall x\in S$

若一个格仅仅在一个算子上良定义，则称为半格(semilattice)。大多数据流分析只需半格即可工作。

分析

哈斯图(Hasse Diagram)：将偏序关系用图的形式展示，如果连边则源点$\leq$汇点

转移(transfer)函数：$F:L\mapsto L$ 由于有序，因此可定义单调转移函数

TODO！！！

参考资料

Allen, F. E., Control Flow Analysis, ACM Sigplan Notices，1970
Cocke, J., Global Common Subexpression Elimination, ACM Sigplan Notices, 1970
Kildall, G., A Unified Approach to Global Program OpGmizations, ACM Symposium on Principles of Programming Languages, 1973
Vyssotsky, V. and P. Wegner, A Graph theoretical Fortran Source Language Analyzer, Technical Report, Bell Laboratories, 1963

9. 循环优化

找到程序中虚拟寄存器/变量对应的实际物理存储位置，寄存器or存储器。

简介

确定哪一个变量应该被保存在寄存器中称为寄存器指派(assignment)
如果变量需要被映射到内存中，则称为溢出(spill)
如果可以消减两个变量之间的移动，则该优化称为联合(coalescing)
MinReg：程序所需的最小寄存器数目
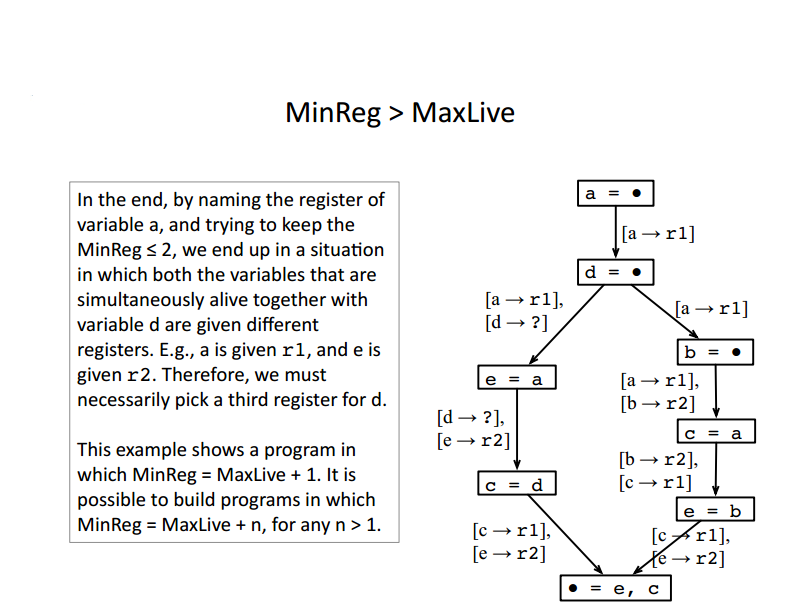
MaxLive：最大同时存活(alive)在程序点中的寄存器数目 MinReg>MaxLive

寄存器分配问题：

给定程序P以及K个通用寄存器，是否存在一种分配方式使得(i)每一个变量在它整个活性范围内获得至少一个寄存器，(ii)同时存活的变量都被分配了不同的寄存器

早在上个世纪80年代，Gregory Chaitin已经证明寄存器分配时NP完备的，通过图染色的方式

希望K染色图，每个相邻结点不同颜色

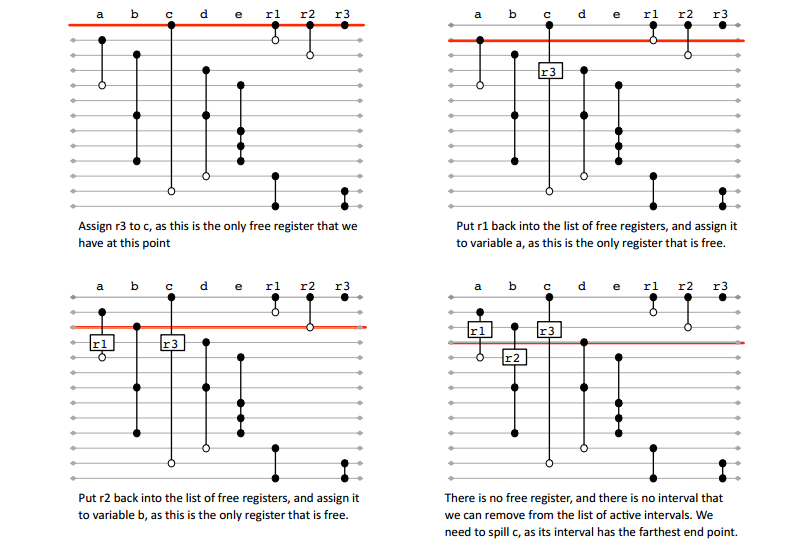
线性扫描(linear scan)

工业级编译器中最流行的一种寄存器分配方法
基于区间图的贪心染色
- 给出一系列的区间，希望找到最少的颜色数量去填涂它们，使得重叠的区间都不同色
- 有最优算法
  
  Algorithmic Graph Theory and Perfect Graphs, 2004
线性扫描不是最优的，但它的最优算法能够给出一个寄存器分配的近似解

图染色(graph coloring)

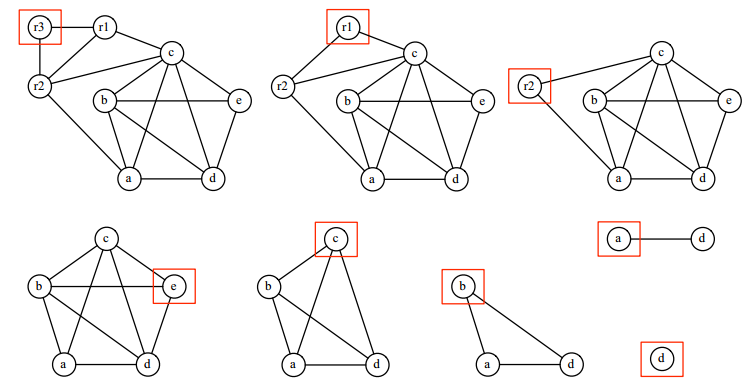
推断图(interference graph)

每一个变量都对应着一个顶点
两个顶点相邻当且仅当它们的活性区间重叠

Kempe的启发式算法

A. Kempe, On the geographical problem of the four colors, 1879 若图包含一个结点v少于K个邻居，令$G’=G\ {m}$，若G’可被染色，则G同样可以被染色

可以不断移除低度的顶点，知道我们只剩下高度的顶点（以预设的K为界），或所有顶点都被移除。后者称为图可被K染色(colorable)。 Kempe

可以用贪心方法按照逆向移出的顺序进行染色，看颜色是否被邻居使用

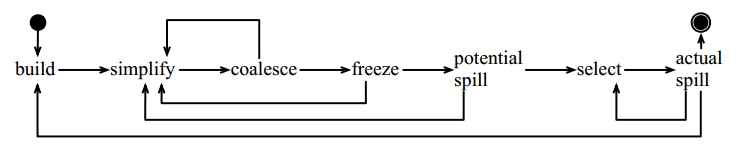
迭代寄存器联合

Iterated Register Coalescing, TOPLAS, 1996

iterated-register-coalescing

参考文献

Chaitin, G., Auslander, M., Chandra, A., Cocke, J., Hopkins, M., and Markstein, P., Register allocation via coloring, Computer Languages, 1981
George, L., and Appel, A., Iterated Register Coalescing, North Holland, TOPLAS, 1996
Poletto, M., and Sarkar, V., Linear Scan Register Allocation, TOPLAS, 1999

10. 静态单赋值(SSA)

静态单赋值(Static Single Assignment, SSA)使得程序里的每个变量都有唯一的定义地点，也即整个程序只包含一处某个变量被赋值。

There have been many smart things in the science of compiler writing, but SSA form is certainly one of the smartest.

大量简化了分析和优化的过程
广泛应用于各种编译器，如gcc, LLVM, Jikes, IonMonkey

简单例子-直线程序

没有分支的程序称为直线(straight-line)程序

将直线程序改写为SSA形式是非常简单的，只需给每个变量加下标即可，新的定义下标加1，如

L0: a = x + y
L1: b = a - 1
L2: a = y + b
L3: b = 4 * x
L4: a = a + b

改写为

L0: a1 = x0 + y0
L1: b1 = a1 - 1
L2: a2 = y0 + b1
L3: b2 = 4 * x0
L4: a3 = a2 + b2

如果遇到分支程序，则需引入Phi函数（就是一个选择器multiplexer），如

b2=Phi(b0,b1)

，代表b2的值可能从b0来也可能从b1来。

TODO

参考文献

SSA最早被Ron Cytron提出
编译器通常用Lengauer/Tarjan的算法找支配子
有很多种变体的SSA形式，最为常见的是pruned SSA形式(Briggs)

Cytron, R. and Ferrante, J. and Rosen, B. and Wegman, M. and Zadeck, F., *An Efficient Method of Computing Static Single Assignment Form”, POPL, 1989
Lengauer, T. and Tarjan, R., A Fast Algorithm for Finding Dominators in a Flowgraph, TOPLAS, 1979
Briggs, P. and Cooper, K. and Harvey, J. and Simpson, L., Practical Improvements to the Construction and Destruction of Static Single Assignment Form, SP&E, 1998

20. 寄存器分配

找到程序中虚拟寄存器/变量对应的实际物理存储位置，寄存器or存储器。

简介

确定哪一个变量应该被保存在寄存器中称为寄存器指派(assignment)
如果变量需要被映射到内存中，则称为溢出(spill)
如果可以消减两个变量之间的移动，则该优化称为联合(coalescing)
MinReg：程序所需的最小寄存器数目
MaxLive：最大同时存活(alive)在程序点中的寄存器数目 MinReg>MaxLive

寄存器分配问题：

给定程序P以及K个通用寄存器，是否存在一种分配方式使得(i)每一个变量在它整个活性范围内获得至少一个寄存器，(ii)同时存活的变量都被分配了不同的寄存器

早在上个世纪80年代，Gregory Chaitin已经证明寄存器分配时NP完备的，通过图染色的方式

希望K染色图，每个相邻结点不同颜色

线性扫描(linear scan)

工业级编译器中最流行的一种寄存器分配方法
基于区间图的贪心染色
- 给出一系列的区间，希望找到最少的颜色数量去填涂它们，使得重叠的区间都不同色
- 有最优算法
  
  Algorithmic Graph Theory and Perfect Graphs, 2004
线性扫描不是最优的，但它的最优算法能够给出一个寄存器分配的近似解

图染色(graph coloring)

推断图(interference graph)

每一个变量都对应着一个顶点
两个顶点相邻当且仅当它们的活性区间重叠

Kempe的启发式算法

A. Kempe, On the geographical problem of the four colors, 1879 若图包含一个结点v少于K个邻居，令$G’=G\ {m}$，若G’可被染色，则G同样可以被染色

可以不断移除低度的顶点，知道我们只剩下高度的顶点（以预设的K为界），或所有顶点都被移除。后者称为图可被K染色(colorable)。 Kempe

可以用贪心方法按照逆向移出的顺序进行染色，看颜色是否被邻居使用

迭代寄存器联合

Iterated Register Coalescing, TOPLAS, 1996

iterated-register-coalescing

参考文献

Chaitin, G., Auslander, M., Chandra, A., Cocke, J., Hopkins, M., and Markstein, P., Register allocation via coloring, Computer Languages, 1981
George, L., and Appel, A., Iterated Register Coalescing, North Holland, TOPLAS, 1996
Poletto, M., and Sarkar, V., Linear Scan Register Allocation, TOPLAS, 1999

24. 循环并行

串行(sequential)程序：不考虑并行因素
并行(parallel)程序：同时跑多个线程或进程

考虑将串行程序编译到并行机器上…

注意：本文考虑的是循环体粒度上的并行，而不是指令粒度上的并行。

并行是否带来收益

如果$O^p+O^d\leq O^s$，则可以并行，其中$O^d$为通信复杂度。

很显然，对于矩阵乘法，当数据规模比较小时，CPU远快于GPU；只有当数据规模变大，GPU才有优势。而对于矩阵加法，通信开销太大导致GPU完全没有优势。

数据重用(reuse)

可以将数组的访问，如X[ai+bj+c,di+ej+f]表示成矩阵形式

\[\begin{bmatrix}a&b\\d&e\end{bmatrix}\times\begin{bmatrix}i\\j\end{bmatrix}+\begin{bmatrix}c\\f\end{bmatrix}\]

迭代空间(iteration space)

即多少重循环，每层循环及其循环变量构成一个维度
若迭代空间有d维，每一个都有$O(N)$的循环技术，那么访问这些秩为k的数组，数据重用$O(N^{d-k})$次

数据依赖

如果两条指令不相关，那么可以直接并行化
若两条指令访问相同位置，且至少有一条是写，则这两条指令相关（但通常我们需要别名分析判断是否同一数组）

简化问题，没有两个数组为别名(alias)。下面是一个简单的例子

N = _getNumPoints(&Points); 
a = malloc(2 * sizeof(double) * N); 
for (i = 0; i < N; i++) { 
    a[2 * i] = _getPoint(&Points, i).x; 
    a[2 * i + 1] = _getPoint(&Points, i).y; 
}

判断是否有依赖关系，即解丢番图(Diophantine)方程

\[2\times i=2\times i'+1\quad\implies\quad 2\times i-2\times i'=1\]

由数论的知识，$gcd(2,2)=2$，但2不整除1，进而无解

多种依赖关系

真(true)依赖：写后读a[i] = …; … = E(a[i – 1]);
反(anti-)依赖：读后写a[i] = ...; … = E(a[i + 1])
输出(output)依赖/重用：写后写a[i] = ...; a[i – 1] = ...

数据依赖的例子 data dependency 但实际上这个例子也是不适合在GPU上跑的，因为每个数据只被重用了两次

免除同步(sync-free)的并行

即各个线程之间不需要通信

若某一维度可以以任何顺序被计算，则称为可交换的(commutative)，例子是丢番图方程解出$i=i’$或$j=j’$等。

参考文献

大多自动并行化循环的工作都诞生于上个世纪八九十年代
Lamport第一个提出循环迭代空间的概念，用其寻找多核并行
上述很多想法都采用自Rice大学的PFC并行器

Allen, R. and K. Kennedy, Automatic Transla>on of Fortran Programs to Vector form, TOPLAS, 1987
Lamport, L., The Parallel Execution of DO Loops, Comm. ACM, 1974
Maydan, D. E., J. L. Hennessy, and M. S. Lam, An Efficient Method for Exact Dependence Analysis, PLDI, 1991
Allen, F. E., M. Burke, P. Charles, R. Cytron, and J. Ferrante, An Overview of the PTRAN Analysis System for Multiprocessing, J. Parallel and Distributed Computing, 1988

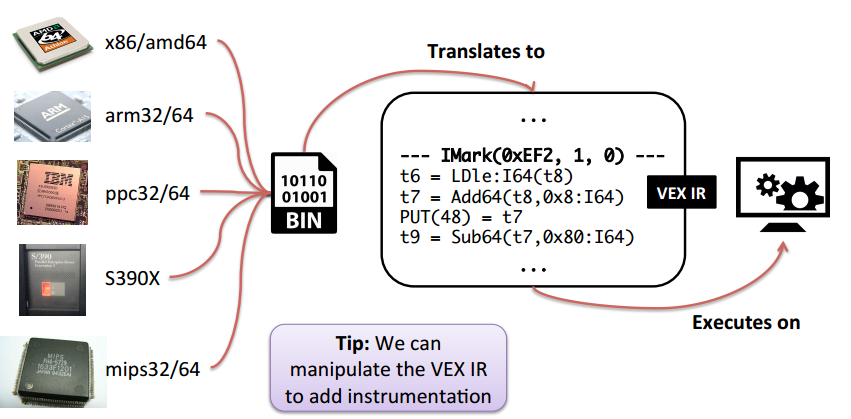
Extra 1. Valgrind

Valgrind是用于动态二进制指令分析(dynamic binary instrumentation, DBI)的框架。（在我院的vmatrix测评系统中也用到，用于动态内存监测，当时坑了不少人…）

动态：执行中的行为，而不是静态的代码结构
二进制：低层次而不是高层次的源代码
工具：通过加减修改指令操控程序执行过程

概要

Valgrind is a program emulator/simulator that allows instructions manipulation/injection.

Memcheck：检查所有内存管理的问题，所有的读写内存操作都被检查，malloc/new/free/delete都被监听(intercept)
Cachegrind：cache分析器(profiler)执行L1、L2 cache详细的模拟(simulation)
Callgrind：cachegrind的扩展，给出更多关于callgraph的信息
Helgrind：线程debugger，用于找出多线程程序中的数据竞争(race)
Massif：堆分析器
DRD：监测多线程C/C++程序中的错误

Valgrind overview

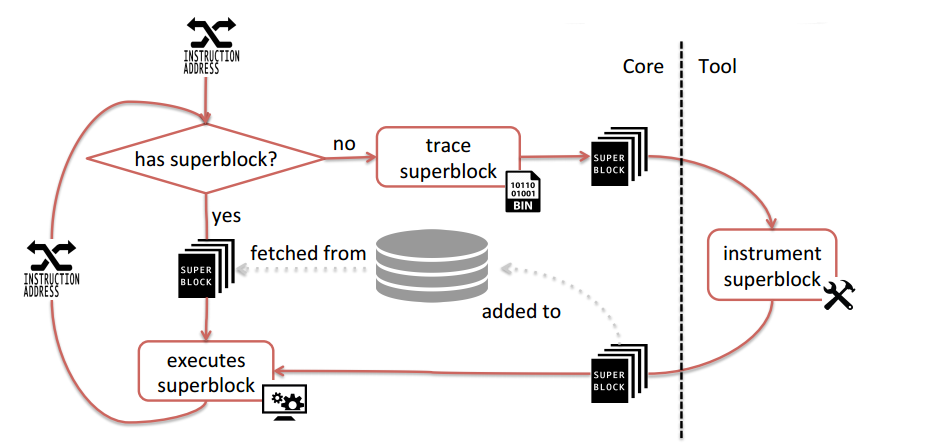
架构

Valgrind结构可以被划分为两个部分

核心(core)
- Low-level infrastructure to support instrumentation
- JIT compiler, memory manager, signal handler, scheduler (for pthreads) - Provides useful services
工具(tool)
- Responsible for the instrumentation
- Requests services from the core
- Is notified of events from the core

Valgrind workflow

Extra 2. 指令级并行

指令级并行(Instruction Level Parallelism, ILP)衡量的是多少操作(operation)能够被计算机程序同时执行，ILP能给内在串行的程序提供并行性。

几种基本的方法获得ILP：

指令流水(pipelining)：每个时刻发射(issue)一条指令，但重叠多条指令
超标量(superscalar)：每个时刻发射多条指令，多个执行单元并行执行

寄存器分配通常希望最小化寄存器资源，这会与并行性产生矛盾，需要协调

基本块内调度

资源限制，拓扑序ASAP，遇到相同层级指令看哪一个离终点更远，则先调度(ALAP)

一般的调度问题是NP完全的，被Richard Karp证明^[3]。

全局调度

通过上移指令实现一条指令多个操作，VLIW(Very Long Instruction Word)机器，但现在很少用

静态性能剖析(static profiling)

猜测每个基本块的使用频率，便于跳转^[5].

不同的启发式算法预测值不同，Dempster-Shafer融合

\[m_1\otimes m_2=\dfrac{m_1\times m_2}{m_1\times m_2+(1-m_1)\times (1-m_2)}\]

参考文献

Hennessy, J. L. and D. A. Patterson, Computer Architecture: A Quantative Approach, Third Edition, 2003
Kuck, D., Y. Muraoka, and S. Chen, On the number of operations simultaneously executable in Fortran-like programs and their resulting speedup, IEEE Transactions on Computers, 1972
Richard Karp, Reducibility Among Combinatorial Problems, 1972
Bernstein, D. and M. Rodeh, Global instruction scheduling for super-scalar machines, PLDI, 1991
Youfeng Wu, J.R. Larus, Static Branch Frequency and Program Profile Analysis, MICRO, 1994

Hongzheng Chen Blog

静态程序分析

1. 简介

课程简介

静态与动态分析

历史

当前的挑战

相关会议与期刊

2. 控制流图

LLVM (Low-Level Virtual Machine)

整体编译流程

简介

LLVM IR

局部优化

DAG优化

窥孔优化(peephole)

局部寄存器分配

参考文献

3. 数据流分析

活性(Liveness)

可用表达式(Available expressions)

很忙表达式(Very busy expressions)

可达性定义(Reaching definitions)

总结：单调框架(The Monotone Framework)

参考文献

4. 工作表算法

用Prolog解限制方程

迭代工作表求解器(iterative worklist solvers)

参考文献

5. 格论

简介

分析

TODO！！！

参考资料

9. 循环优化

简介

线性扫描(linear scan)

图染色(graph coloring)

迭代寄存器联合

参考文献

10. 静态单赋值(SSA)

简单例子-直线程序

参考文献

20. 寄存器分配

简介

线性扫描(linear scan)

图染色(graph coloring)

迭代寄存器联合

参考文献

24. 循环并行

并行是否带来收益

数据重用(reuse)

数据依赖

免除同步(sync-free)的并行

参考文献

Extra 1. Valgrind

概要

架构

Extra 2. 指令级并行

基本块内调度

全局调度

静态性能剖析(static profiling)

参考文献

Related Posts

静态程序分析 (SPA) Mar 24th, 2020

程序综合与编译 Feb 1st, 2020

LLVM Feb 22nd, 2019