Hongzheng Chen Blog

图表示学习（2）- 图神经网络

Feb 10th, 2020  0

这是图表示学习(representation learning)的第二部分——图神经网络(graph neural network, gnn)，主要涉及GCN [ICLR’17]、GraphSAGE [NeurIPS’17]、GAT [ICLR’18]和C&S [Arxiv:2010.13993]三篇论文。

关于图数据挖掘/表示学习的内容强烈建议去看Stanford Jure Leskovec的Tutorial - Representation Learning on Networks (WWW’18)。

前一节的图嵌入方法都是非常浅(shallow)的，通过学习得到一个矩阵/查找表，来得到结点的嵌入向量。但是这种方法有以下几点缺陷：

  • 需要$O(\vert V\vert)$的参数量：没有任何参数的共享，所有结点都只有它自己的嵌入向量
  • 内在传导(transductive)：很难生成一个没见过的结点的嵌入
  • 无监督方法：没有将结点特征有机整合，而只是关注于图结构

因此我们希望采用更深的方法来得到结点嵌入，最好是直接学习得到一个连续函数，而不是表格映射（这个发展路径其实跟当年强化学习到深度强化学习的过程是类似的）。

回忆稠密网格下的卷积1，原来格点上的数据通过与卷积核的参数分别相乘求和，最后邻居格点的加权和都会汇总到中心格点上。由于卷积核滑过整个图片，而其中的参数多次被使用（参数共享），因此可以更好捕获图片的细节特征。

类比到图数据也是一样的，核心思想是从邻居结点整合特征，只是邻居不再是原来的网格紧邻，且每个结点的邻居数目也不一定相同。

聚合特征之后通过黑箱网络，对输出拟合。如下图所示，0层即输入层，也即输入特征。

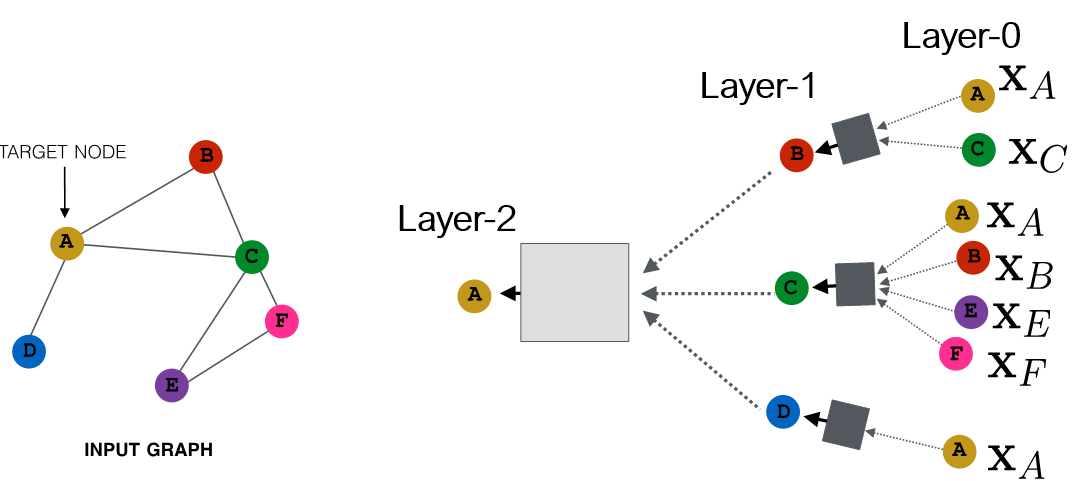
所以关键在于黑箱中是什么，也即聚合信息的方法。

最简单的方式，取平均然后过神经网络。

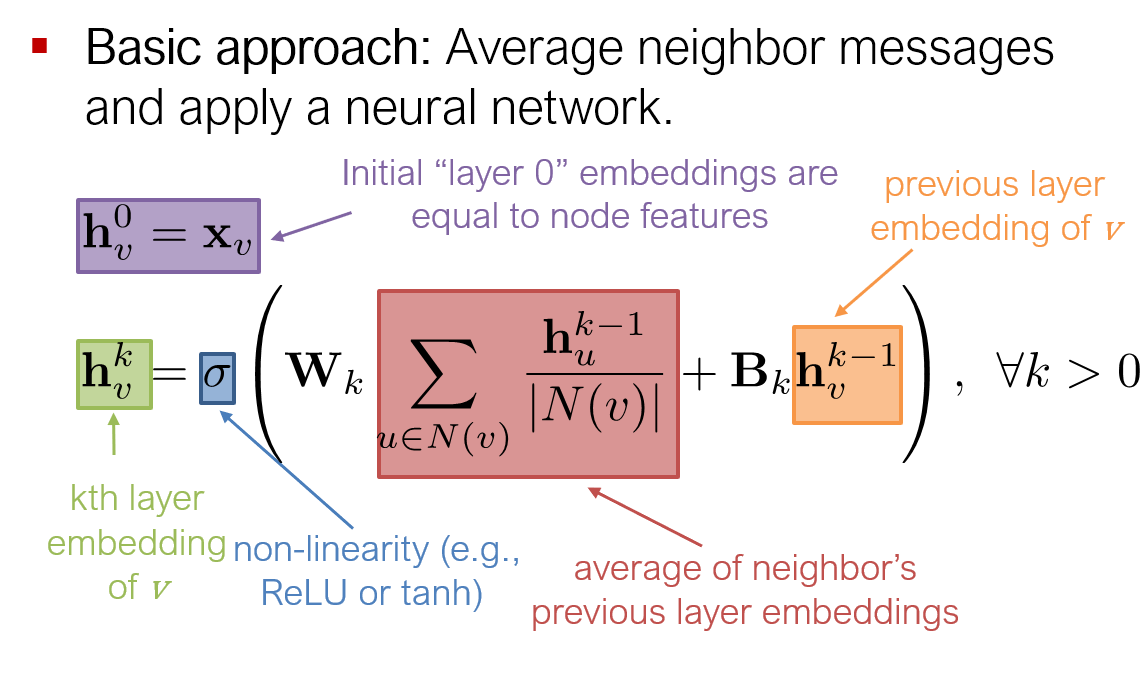
或用矩阵的形式表示（$H^{(0)}=X$）

\[H^{(k+1)}=f(H^{(k)},A)=\sigma(AH^{(k)}W^{(k)})\]

其中$A\in\mathbb{R}^{n\times n}$为邻接阵，$H\in\mathbb{R}^{n\times d_{in}}$为特征阵（注意这里一行为一个结点的嵌入向量，与前面的向量写法不同），$W\in\mathbb{R}^{d_{in}\times d_{out}}$为每一层的训练权重矩阵（注意到这里是全层共享参数）。这里可划分为两个步骤：消息聚合与特征更新。

第一部分消息聚合，即$A$与$H$左乘（稀疏矩阵乘稠密矩阵，图计算），相当于考虑$A$的第$i$行，即第$i$个结点$v_i$，与其邻接的结点的第$j$个特征进行聚合，得到$(i,j)$矩阵元素。

\[(AH^{(k)})_{ij}=\sum_{l}a_{il}h_{lj}=\sum_{v_l\in \mathcal{N}(v_i)}h_{v_l j} \implies \mathbf{h}_i=\sum_{v_l\in \mathcal{N}(v_i)}\mathbf{h}_{l}\]

第二部分特征更新，将聚合的特征与参数矩阵相乘（稠密阵乘稠密阵，深度学习）

\[\mathbf{h}_i^{(k+1)}=\left(\sum_{v_l\in \mathcal{N}(v_i)}\mathbf{h}_{l}^{(k)}\right)W^{(k)} =\sum_{v_l\in \mathcal{N}(v_i)}\mathbf{h}_{l}^{(k)}W^{(k)}\]

由于矩阵乘符合结合律，故消息聚合与特征更新顺序可以互换。 如果先聚合再算更新，则对于结点$i$来说需要做$d_i$次维度$d_{in}$的加法与$1$次乘法$d_{in}\mapsto d_{out}$，由握手定理，全图一共是$2|E|$次加法与$|V|$次矩阵向量乘（或$1$次矩阵矩阵乘）；而先更新再聚合，对于结点$i$需要做$d_i$次维度$d_{out}$的加法与$d_i$次乘法，全图则是$O(|E|)$的时间复杂度。但事实上由于邻居结点会被多个结点共享，因此用矩阵矩阵乘提前算出$H^{(k)}W^{(k)}$，再去索引聚合，乘法次数同样是$1$次。

这里就可以采用前面的无监督方法作为损失函数，或者用有监督的模型来构造。

总的来说，GNN的模型构造分为以下四步走：

  1. 定义邻居聚集函数（黑箱中是什么）
  2. 定义结点嵌入上的损失函数$L(z_u)$
  3. 对一系列的结点计算图进行训练
  4. 生成结点嵌入

注意到$W_k$和$B_k$都是共享参数，因此模型参数的复杂度是关于$\vert V\vert$次线性的。同时，这种方法可以扩展到未见过的结点。

GCN2

关于GCN的详细介绍，可见论文一作的博客。

依照上文的矩阵表示法，

\[H^{(k+1)}=f(H^{(k)},A)=\sigma(AH^{(k)}W^{(k)})\]

尽管该模型已经很强大，但是仍然存在以下两个问题，这也是文2所要解决的：

  1. 注意到$AH^{(k)}$消息聚合时并未将自身考虑进去，因此可以简单地给每个结点添加自环，即$\hat{A}=A+I$
  2. 每个结点的度并不相同，导致$AH^{(k)}$计算时会改变特征向量的比例(scale)，那么简单的想法是类似PageRank一样对邻接阵$A$的每一行归一化，即$D^{-1}A$，其中$D$是度对角阵（取逆相当于对角线上元素，即每个结点的度数，直接取倒数）。而如果采用对称的归一化技术（即出入度都考虑），那就得到$D^{-1/2}AD^{-1/2}$。（对称阵的计算可见图论基础）

进而得到GCN的传播规则

\[H^{(k+1)}=f(H^{(k)},A)=\sigma\left(\hat{D}^{-\frac{1}{2}}\hat{A}\hat{D}^{-\frac{1}{2}}H^{(k)}W^{(k)}\right)\]

用向量形式来写即

\[\mathbf{h}_v^{(k+1)}=\sigma\left(\sum_{u\in N(v)\cup v}\frac{\mathbf{h}_u^{(k)}}{\sqrt{|N(u)||N(v)|}}W^{(k)}\right)\]

总的时间复杂度是$O(\vert E\vert)$。

GCN很强的一点在于，它还没训练就已经达到DeepWalk的水准了。比如下图展示的是未训练的3层GCN结点嵌入情况，矩阵都是随机初始化的。

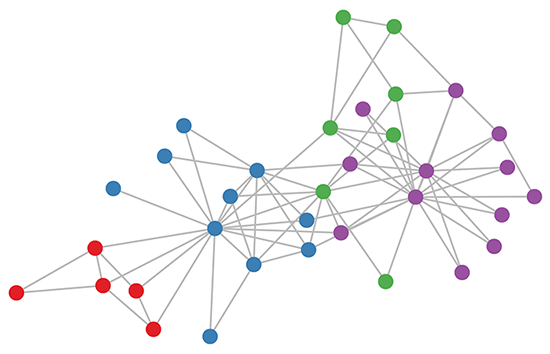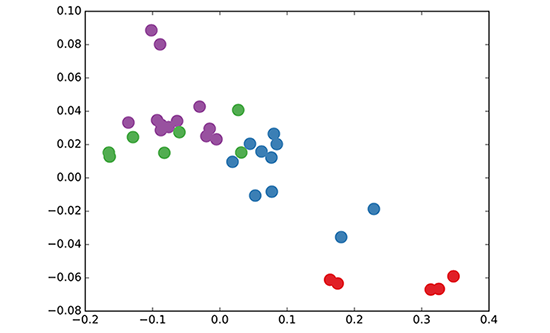至于为什么是卷积，想想卷积核在稀疏邻接矩阵上划过，聚合时实际上就相当于做卷积了。

GraphSAGE3

GraphSAGE (SAmple & aggreGatE)则是进一步将聚合的思想一般化，之前的聚合函数都是取平均，那现在我采用任意的聚合函数，得到

\[h_v^{(k+1)}=\sigma([W_k\cdot \mathop{AGG}(\{\mathbb{h}_{u}^{(k)},\forall u\in N(v)\}),B_k\mathbb{h}_v^{(k)}])\]

注意中括号表示两个向量（自嵌入+邻居嵌入）直接合并，邻居在GraphSAGE中并不取全部，而是随机取固定数目的邻居。

聚合函数就可以取

  • 平均：最原始方案
\[\mathop{AGG}=\sum_{u\in N(u)}\frac{\mathbb{h}_{u}^{(k)}}{|N(v)|}\]
  • 池化：$\gamma$为元素间(element-wise)平均/最值
\[\mathop{AGG}=\gamma(\{Q\mathbb{h}_{u}^{(k)},\forall u\in N(v)\})\]
  • LSTM：$\pi$为随机置换(permutation)
\[\mathop{AGG}=LSTM([\mathbb{h}_{u}^{(k)},\forall u\in\pi(N(v))])\]

通常GCN和GraphSAGE只需两三层深即可。

从某种意义上，GCN有点像循环神经网络，因为GCN在每一层上都是共享参数的，而每一层就是一整个graph平展开来，每一层的计算都是传播一hop的计算，只有当这一层计算完了（图遍历完了），才进入到下一层的计算。

gnn

从GraphSAGE的伪代码就更加能体会到这一点：外层做$K$次循环，内层遍历所有结点做消息传递（这其实相当于对整个无向图做一次BFS）

在GraphSAGE中也引进了一个新的概念–归纳式学习(inductive learning)，即通过采样与聚合中心节点的邻居信息来生成节点embedding，这是可以适用于不同graph inputs的（结点或边可以后面再持续插入）；而传统的GNN算法是直推式学习(transductive learning)，即在训练节点embedding时需加载所有节点信息。

GAT 4

回忆NLP中的encoder-decoder模型，由于encoder需要将一整个句子的信息压缩到一个高维空间向量，再送入decoder进行解码，这一个高维空间向量的负担将会非常大，因此研究者就考虑让机器学会判断句子中的不同部分的重要性，从而在解码时更加有针对性地获取特征，此即attention的思想5。

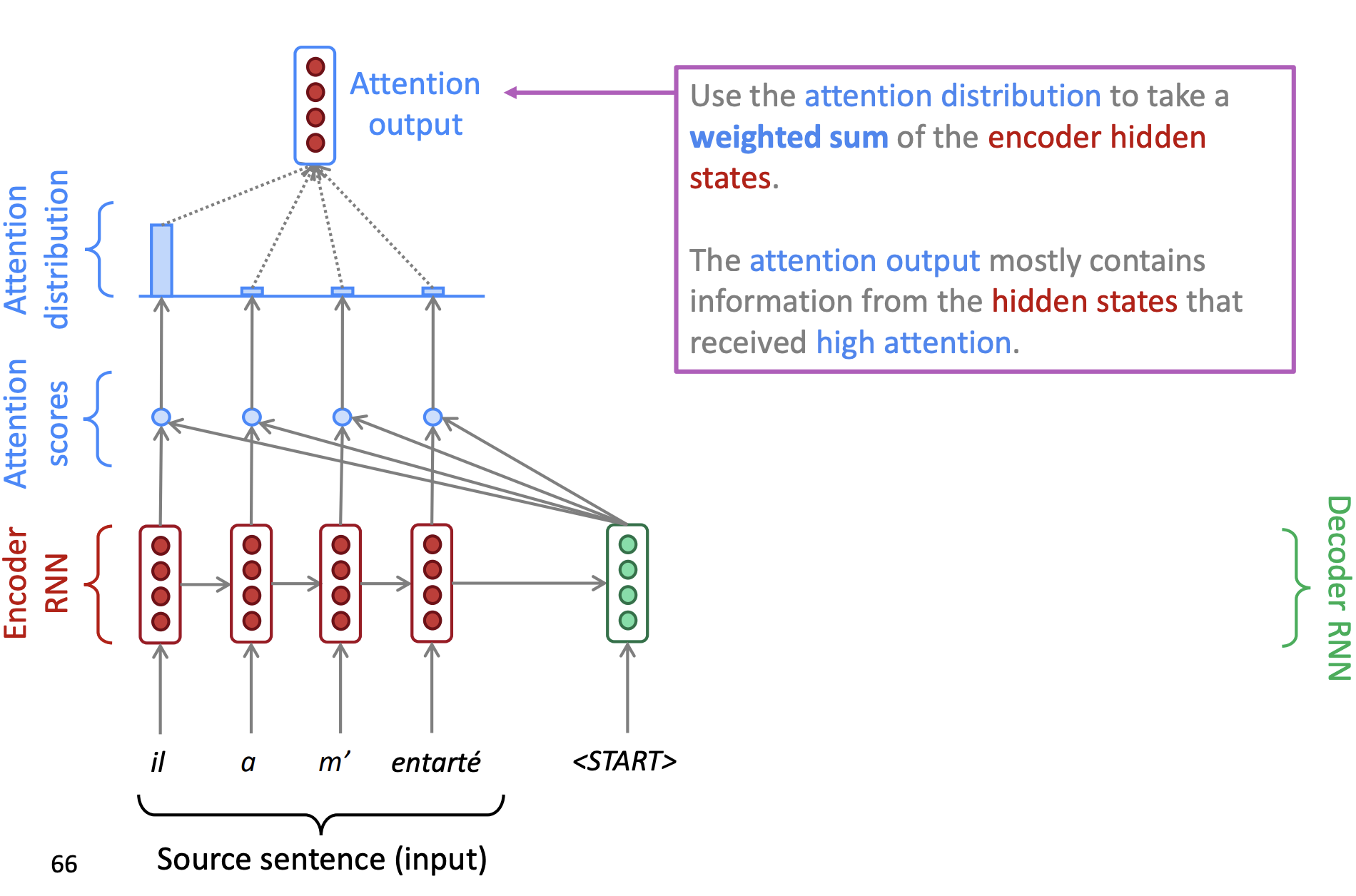
放到graph中也是类似，原始聚合公式中将不同结点等同对待，因此可以添加一个attention模块，让机器自己学习不同结点的重要性$\alpha_{il}$（$v_l$对$v_i$的重要性）。

\[\mathbf{h}_i^{(k+1)}=\sum_{v_l\in \mathcal{N}(v_i)}\alpha_{il}\mathbf{h}_{l}^{(k)}W^{(k)}\]

重要性度量可以是$\phi(h_i,h_l)$（注意这里用了原始特征向量$h_\cdot$），其中$\phi$为可学习的函数，GAT论文中直接采用了单层神经网络。

由于重要性的scale可能不同，因此可以通过归一化方法得到合理的重要性度量指标，这里采用了softmax

\[\alpha_{il}=\frac{\exp(\phi(h_i,h_l))}{\sum_{k\in\mathcal{N}(v_i)}\exp(\phi(h_i,h_k))}\]

更进一步，可以采用多头(multi-head)的attention机制，不同head采用不同$\alpha$，最后再将这些结果合并起来或者取平均。

Correct & Smooth (C&S) 6

这篇paper在2020年10月的时候霸榜了OGB的几个数据集，核心是在claim我们不需要GNN这么复杂的模型，用简单的MLP加上一些后处理技巧就可以做到很好的效果了。

分为三步走，第一步用MLP直接暴力拟合（不考虑图结构），第二步correct，第三步smooth。

假设特征矩阵为$X\in\mathbb{R}^{n\times p}$，目标矩阵$Y\in\mathbb{R}^{n\times c}$为one-hot encoding，第一步MLP则是学一个函数$f$使得最小化损失函数之和

\[\sum l(f(X_i),Y_i)\]

可以想象经过$f$得到的是一个softmax的概率，即为各个类别的预测值$\hat{Y}_i$，此为base prediction。

第二步correct，即算预测值和真实值的残差$E=\hat{Y}-Y$，然后用标签传播优化$E$（此时引入图结构，具体优化目标见论文）。这里的idea在于误差应该沿着图的边正相关（base prediction to be positively correlated along edges in the graph），换句话说结点$i$有误差，则其邻居也应该有相似的误差。这一步会得到一个新的估计$\hat{Y}^{(r)}$

第三步smooth，idea是相邻的点应该有相似的label，这样又可以得到另外一个优化函数，再通过另一轮label propagation得到最终结果。

Other Resources

Reference

  1. Petar Veličković, https://petar-v.com/GAT/ ↩

  2. Thomas N. Kipf, Max Welling (Amsterdam), Semisupervised Classification with Graph Convolutional Networks, ICLR, 2017 (Most cited publication) ↩ ↩2

  3. William L. Hamilton, Rex Ying, Jure Leskovec (Stanford), Inductive Representation Learning on Large Graphs, NeurIPS, 2017 ↩

  4. Petar Veličković, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Liò and Yoshua Bengio, Graph Attention Networks, ICLR, 2018 ↩

  5. Stanford CS224n: Natural Language Processing with Deep Learning, Machine Translation ↩

  6. Qian Huang, Horace He, Abhay Singh, Ser-Nam Lim, Austin R. Benson (Cornell), Combining Label Propagation and Simple Models Outperforms Graph Neural Networks, Arxiv:2010.13993, 2020 (Code) ↩

Related Posts