TVM - GEMM优化

Mar 20th, 2020 0

本文记录如何使用TVM v0.6在CPU上优化GEMM，节选自TVM官方教程。类似地，可参考Vivado HLS优化GEMM的方法。其中涉及到局部性(locality)的问题会详细进行分析。

朴素GEMM

我们可以将朴素GEMM，写成下列这种伪代码形式，用爱因斯坦求和记号(einsum)即$C_{ij}=A_{ik}B_{kj}$

for (i, 0, M)
  for (j, 0, N)
    for (k, 0, K)
      C[i][j] += A[i][k] * B[k][j]

可先写出朴素的NumPy和TVM实现，并比较它们的运行时间。

输出结果如下，可以看到numpy的速度（调用Intel MKL）是比裸GEMM实现$O(n^3)$要快得多的。

produce C {
  for (x, 0, 1024) {
    for (y, 0, 1024) {
      C[((x*1024) + y)] = 0f
      for (k, 0, 1024) {
        C[((x*1024) + y)] = (C[((x*1024) + y)] + (A[((x*1024) + k)]*B[((k*1024) + y)]))
      }
    }
  }
}

Numpy running time: 0.007936
Baseline: 2.890711

接下来我们仔细分析下其中的瓶颈。

循环重排(reordering)

注意到我们访问数据的模式，对于C和A矩阵来说，我们都是采用逐行遍历数据的方式，而对于B则是逐列遍历数据。

traversal order

但是通常情况下，在计算机里我们采用的都是行优先(row-major)存储。如果一个cache line可以装8*int(32B)，那么按行遍历（正Z型），可以保证每8个访存只有第1个元素miss；而按列遍历，很有可能读入的行数据没有用到就被驱逐出去了，miss rate为100\%。

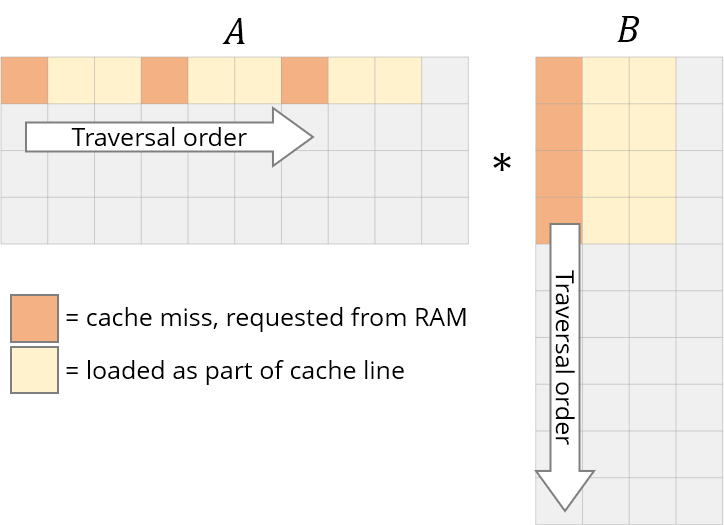
cache miss

故一个简单但极其有效的方式就是修改遍历顺序，即循环重排。

for (i, 0, M)
  for (k, 0, K)
    for (j, 0, N)
      C[i][j] = A[i][k] * B[k][j]

计算结果显然是一样的，但是重排之后，B也变成了行遍历，进而提升了空间局部性，如下图。

row traversal

我们分析下这种模式：

重复扫C数组K次，每次扫同一行（时间局部性好）
A的时间局部性同样很高，因为A[i][k]被重复用了N次
B则是确保了行优先存储下的空间局部性

只需要在TVM中添加一行

s[C].reorder(C.op.axis[0], k, C.op.axis[1])

即可实现循环重排。计算结果如下，可以看到k循环确实放到了中间层，并且速度提升了15倍！

produce C {
  for (x, 0, 1024) {
    for (y.init, 0, 1024) {
      C[((x*1024) + y.init)] = 0f
    }
    for (k, 0, 1024) {
      for (y, 0, 1024) {
        C[((x*1024) + y)] = (C[((x*1024) + y)] + (A[((x*1024) + k)]*B[((k*1024) + y)]))
      }
    }
  }
}

Opt1: 0.190684

循环平铺(tiling)

再来仔细分析下GEMM的三重循环，虽然我们改变了循环顺序，从而提升了C数组的时间局部性，但是要让这种局部性成立，必须使前面加载进来的元素不会被替换出去。

还是考虑仅一个cache line里8个int的例子，最好的情况是1-8一直驻留在cache中，要不然当访问到9时，1就会被剔除。这样来看，最好的情况则是保证数组遍历始终控制在一个很小的范围内，而这个范围由cache大小决定，以保证数组元素能全部驻留在cache中。

类似的道理可分析A和B数组，当A进入到下一行时，B又得从头重新遍历整个矩阵，那么它的重用度/时间局部性是非常差的，因为cache的容量限制，加载进来的元素在后面计算时会被驱逐，当要用时才重新加载回来，造成频繁的cache抖动(thrashing)。

因此解决方式上面已经提了，就是对cache进行分块(blocking)，通过计算小矩阵来提升重用性，确保所有数据都能落在cache中。

将大矩阵C分块，每个块大小64*64（超参数需要尝试），这样一共占用$2^6\cdot 2^6\cdot 4B=2^{14}B=16KB$的cache容量（按float来计算），而L1 cache现在都做得非常大了，比如我电脑Intel Core i7 CPU的L1 cache已经达到256KB，存储这些数据绰绰有余。

i和j维度可以用tile进行分块，k由于是单一维度，故用split将一个轴分划为两个轴（分割因子为factor），进而可以写出对应的TVM代码。

# Blocking by loop tiling
bn = 64
xo, yo, xi, yi = s[C].tile(C.op.axis[0], C.op.axis[1], x_factor=bn, y_factor=bn)
k, = s[C].op.reduce_axis
ko, ki = s[C].split(k, factor=4)

# Hoist reduction domain outside the blocking loop
s[C].reorder(xo, yo, ko, ki, xi, yi)

运行结果如下，可以看到提升并不是很明显。~~（这说明调参也是技术活）~~

produce C {
  for (x.outer, 0, 16) {
    for (y.outer, 0, 16) {
      for (x.inner.init, 0, 64) {
        for (y.inner.init, 0, 64) {
          C[((((x.outer*65536) + (x.inner.init*1024)) + (y.outer*64)) + y.inner.init)] = 0f
        }
      }
      for (k.outer, 0, 128) {
        for (k.inner, 0, 8) {
          for (x.inner, 0, 64) {
            for (y.inner, 0, 64) {
              C[((((x.outer*65536) + (x.inner*1024)) + (y.outer*64)) + y.inner)] = (C[((((x.outer*65536) + (x.inner*1024)) + (y.outer*64)) + y.inner)] + (A[((((x.outer*65536) + (x.inner*1024)) + (k.outer*8)) + k.inner)]*B[((((k.outer*8192) + (k.inner*1024)) + (y.outer*64)) + y.inner)]))
            }
          }
        }
      }
    }
  }
}

Opt2: 0.175358

向量化(vectorization)

现代的CPU大多都支持SIMD，因此可以通过向量化的方式，来加速计算。

SIMD

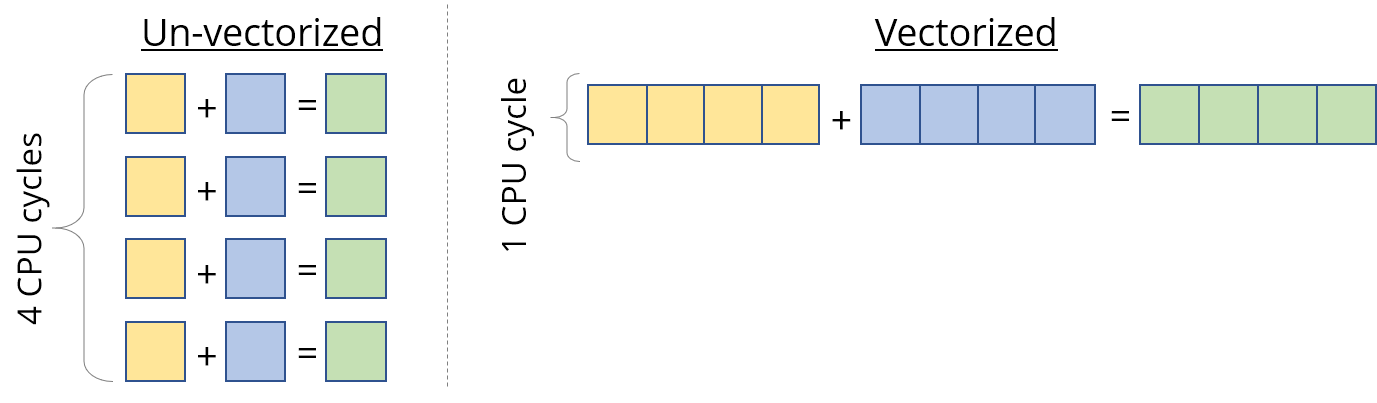
在TVM中只需添加下面一行即可实现最内层循环的向量化。

s[C].vectorize(yi)

结果如下，同样没有提升，很大原因是构造SIMD也是有数据搬移开销的。

produce C {
  for (x.outer, 0, 16) {
    for (y.outer, 0, 16) {
      for (x.inner.init, 0, 64) {
        C[ramp((((x.outer*65536) + (x.inner.init*1024)) + (y.outer*64)), 1, 64)] = x64(0f)
      }
      for (k.outer, 0, 64) {
        for (k.inner, 0, 16) {
          for (x.inner, 0, 64) {
            C[ramp((((x.outer*65536) + (x.inner*1024)) + (y.outer*64)), 1, 64)] = (C[ramp((((x.outer*65536) + (x.inner*1024)) + (y.outer*64)), 1, 64)] + (x64(A[((((x.outer*65536) + (x.inner*1024)) + (k.outer*16)) + k.inner)])*B[ramp((((k.outer*16384) + (k.inner*1024)) + (y.outer*64)), 1, 64)]))
          }
        }
      }
    }
  }
}

Opt3: 0.224174

注意到现在B的访问模式是序列的，而A变成了一列列的访问，这对cache不友好，因此通过改变ki和xi的顺序，可以让其变得友好些，即

s[C].reorder(xo, yo, ko, xi, ki, yi)

这回可以看到，运行时间又缩短了一半。

produce C {
  for (x.outer, 0, 16) {
    for (y.outer, 0, 16) {
      for (x.inner.init, 0, 64) {
        C[ramp((((x.outer*65536) + (x.inner.init*1024)) + (y.outer*64)), 1, 64)] = x64(0f)
      }
      for (k.outer, 0, 128) {
        for (x.inner, 0, 64) {
          for (k.inner, 0, 8) {
            C[ramp((((x.outer*65536) + (x.inner*1024)) + (y.outer*64)), 1, 64)] = (C[ramp((((x.outer*65536) + (x.inner*1024)) + (y.outer*64)), 1, 64)] + (x64(A[((((x.outer*65536) + (x.inner*1024)) + (k.outer*8)) + k.inner)])*B[ramp((((k.outer*8192) + (k.inner*1024)) + (y.outer*64)), 1, 64)]))
          }
        }
      }
    }
  }
}

Opt4: 0.107459

数组打包(packing)

因为前面我们已经执行了tiling，虽然这可以提升局部性，但是行与行之间的元素依然没有存储在一起，需要跳掉后面的元素才能访问到。因此，比较好的方法则是改变数组的排列方式，从而确保在同一个block里的元素在顺序内存里也是连续的。

array packing

对应的TVM代码如下。

# We have to re-write the algorithm slightly.
packedB = tvm.compute((N / bn, K, bn), lambda x, y, z: B[y, x * bn + z], name='packedB')
C = tvm.compute((M, N),
                lambda x, y: tvm.sum(A[x, k] * packedB[y // bn, k, tvm.indexmod(y, bn)], axis=k),
                name = 'C')

s = tvm.create_schedule(C.op)

# tiling
# spilting
# reorder
# vertorize

x, y, z = s[packedB].op.axis
s[packedB].vectorize(z)
s[packedB].parallel(x)

运行结果如下，这里稍微改了一下超参数（bn=32, factor=4），但性能还是没有显著提升。

// attr [packedB] storage_scope = "global"
allocate packedB[float32x32 * 32768]
produce packedB {
  parallel (x, 0, 32) {
    for (y, 0, 1024) {
      packedB[ramp(((x*32768) + (y*32)), 1, 32)] = B[ramp(((y*1024) + (x*32)), 1, 32)]
    }
  }
}
produce C {
  for (x.outer, 0, 32) {
    for (y.outer, 0, 32) {
      for (x.inner.init, 0, 32) {
        C[ramp((((x.outer*32768) + (x.inner.init*1024)) + (y.outer*32)), 1, 32)] = x32(0f)
      }
      for (k.outer, 0, 256) {
        for (x.inner, 0, 32) {
          for (k.inner, 0, 4) {
            C[ramp((((x.outer*32768) + (x.inner*1024)) + (y.outer*32)), 1, 32)] = (C[ramp((((x.outer*32768) + (x.inner*1024)) + (y.outer*32)), 1, 32)] + (x32(A[((((x.outer*32768) + (x.inner*1024)) + (k.outer*4)) + k.inner)])*packedB[ramp((((y.outer*32768) + (k.outer*128)) + (k.inner*32)), 1, 32)]))
          }
        }
      }
    }
  }
}

Opt5: 0.109478

写缓存(cache)

在blocking之后，写C数组是按块写的，内存访问模式并非序列(sequential)，因此可以通过利用一个序列cache来存储所有的block结果，然后当block结果都出来时再写到C中。TVM代码如下。

# Allocate write cache
CC = s.cache_write(C, 'global')

xo, yo, xi, yi = s[C].tile(C.op.axis[0], C.op.axis[1], x_factor=bn, y_factor=bn)

# Write cache is computed at yo
s[CC].compute_at(s[C], yo)
# New inner axes
xc, yc = s[CC].op.axis

k, = s[CC].op.reduce_axis
ko, ki = s[CC].split(k, factor=4)
s[CC].reorder(ko, xc, ki, yc)
s[CC].unroll(ki)
s[CC].vectorize(yc)

结果又是做了负向优化…

// attr [packedB] storage_scope = "global"
allocate packedB[float32x32 * 32768]
// attr [C.global] storage_scope = "global"
allocate C.global[float32 * 1024]
produce packedB {
  parallel (x, 0, 32) {
    for (y, 0, 1024) {
      packedB[ramp(((x*32768) + (y*32)), 1, 32)] = B[ramp(((y*1024) + (x*32)), 1, 32)]
    }
  }
}
produce C {
  for (x.outer, 0, 32) {
    for (y.outer, 0, 32) {
      produce C.global {
        for (x.c.init, 0, 32) {
          C.global[ramp((x.c.init*32), 1, 32)] = x32(0f)
        }
        for (k.outer, 0, 256) {
          for (x.c, 0, 32) {
            C.global[ramp((x.c*32), 1, 32)] = (C.global[ramp((x.c*32), 1, 32)] + (x32(A[(((x.outer*32768) + (x.c*1024)) + (k.outer*4))])*packedB[ramp(((y.outer*32768) + (k.outer*128)), 1, 32)]))
            C.global[ramp((x.c*32), 1, 32)] = (C.global[ramp((x.c*32), 1, 32)] + (x32(A[((((x.outer*32768) + (x.c*1024)) + (k.outer*4)) + 1)])*packedB[ramp((((y.outer*32768) + (k.outer*128)) + 32), 1, 32)]))
            C.global[ramp((x.c*32), 1, 32)] = (C.global[ramp((x.c*32), 1, 32)] + (x32(A[((((x.outer*32768) + (x.c*1024)) + (k.outer*4)) + 2)])*packedB[ramp((((y.outer*32768) + (k.outer*128)) + 64), 1, 32)]))
            C.global[ramp((x.c*32), 1, 32)] = (C.global[ramp((x.c*32), 1, 32)] + (x32(A[((((x.outer*32768) + (x.c*1024)) + (k.outer*4)) + 3)])*packedB[ramp((((y.outer*32768) + (k.outer*128)) + 96), 1, 32)]))
          }
        }
      }
      for (x.inner, 0, 32) {
        for (y.inner, 0, 32) {
          C[((((x.outer*32768) + (x.inner*1024)) + (y.outer*32)) + y.inner)] = C.global[((x.inner*32) + y.inner)]
        }
      }
    }
  }
}

Opt6: 0.115978

并行化(parallelism)

最后可以利用多线程技术，在TVM中同样只用一行代码。

s[C].parallel(xo)

得到结果如下，终于达到0.1s以内。

// attr [packedB] storage_scope = "global"
allocate packedB[float32x32 * 32768]
produce packedB {
  parallel (x, 0, 32) {
    for (y, 0, 1024) {
      packedB[ramp(((x*32768) + (y*32)), 1, 32)] = B[ramp(((y*1024) + (x*32)), 1, 32)]
    }
  }
}
produce C {
  parallel (x.outer, 0, 32) {
    // attr [C.global] storage_scope = "global"
    allocate C.global[float32 * 1024]
    for (y.outer, 0, 32) {
      produce C.global {
        for (x.c.init, 0, 32) {
          C.global[ramp((x.c.init*32), 1, 32)] = x32(0f)
        }
        for (k.outer, 0, 256) {
          for (x.c, 0, 32) {
            C.global[ramp((x.c*32), 1, 32)] = (C.global[ramp((x.c*32), 1, 32)] + (x32(A[(((x.outer*32768) + (x.c*1024)) + (k.outer*4))])*packedB[ramp(((y.outer*32768) + (k.outer*128)), 1, 32)]))
            C.global[ramp((x.c*32), 1, 32)] = (C.global[ramp((x.c*32), 1, 32)] + (x32(A[((((x.outer*32768) + (x.c*1024)) + (k.outer*4)) + 1)])*packedB[ramp((((y.outer*32768) + (k.outer*128)) + 32), 1, 32)]))
            C.global[ramp((x.c*32), 1, 32)] = (C.global[ramp((x.c*32), 1, 32)] + (x32(A[((((x.outer*32768) + (x.c*1024)) + (k.outer*4)) + 2)])*packedB[ramp((((y.outer*32768) + (k.outer*128)) + 64), 1, 32)]))
            C.global[ramp((x.c*32), 1, 32)] = (C.global[ramp((x.c*32), 1, 32)] + (x32(A[((((x.outer*32768) + (x.c*1024)) + (k.outer*4)) + 3)])*packedB[ramp((((y.outer*32768) + (k.outer*128)) + 96), 1, 32)]))
          }
        }
      }
      for (x.inner, 0, 32) {
        for (y.inner, 0, 32) {
          C[((((x.outer*32768) + (x.inner*1024)) + (y.outer*32)) + y.inner)] = C.global[((x.inner*32) + y.inner)]
        }
      }
    }
  }
}

Opt7: 0.052135

比原来的baseline版本提升了58倍，但距离NumPy的MKL版本依然存在6.25倍的距离。

References

TVM Tutorial: How to optimize GEMM on CPU
TVM Tutorial: Schedule Primitives in TVM
CSAPP第5章：优化程序性能，第6章：存储器层次结构
Manas Sahni, Anatomy of a High-Speed Convolution, 中文

Hongzheng Chen Blog

TVM - GEMM优化

朴素GEMM

循环重排(reordering)

循环平铺(tiling)

向量化(vectorization)

数组打包(packing)

写缓存(cache)

并行化(parallelism)

References

Related Posts

HLS for Deep Learning Applications Oct 15th, 2020

Binary Neural Network (BNN) May 1st, 2020

TVM - Relay IR Pass Apr 2nd, 2020