Hongzheng Chen Blog
Binary Neural Network (BNN)
May 1st, 2020 0本文简要记录二值神经网络(BNN)的基本原理及计算方式。
基本原理
BNN与CNN最大的区别在于矩阵乘法的处理,也就是卷积层和全连接层,都采用量化的方式,如下用+1和-1两个值来表示。(注意这里没有0,所以实际padding的部分需要忽略不算)
| ${x}$ | ${y}$ | ${x}\cdot{y}$ |
|---|---|---|
| -1 | -1 | +1 |
| -1 | +1 | -1 |
| +1 | -1 | -1 |
| +1 | +1 | +1 |
由于+1和-1需要2位表示,为了方便硬件实现,可改写为下面的同或(XNOR)操作,只会出现0和1,这样就可以用1位表示,并且可以使用位运算。
| $\hat{x}$ | $\hat{y}$ | $\hat{x}\odot\hat{y}$ |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
在算向量乘法时即依据下面的计算公式,其中$L$为点乘向量的长度。
\[\begin{aligned} \mathbf{x}\cdot\mathbf{y} &=\sum_{i=0}^L x_i\cdot y_i\\ &=\sum_{i=0}^L (2(\hat{x}_i\odot \hat{y}_i)-1)\\ &=2\sum_{i=0}^L (\hat{x}_i\odot\hat{y}_i) - L\qquad\text{XNOR}\\ &=2\sum_{i=0}^L (1-(\hat{x}_i\oplus\hat{y}_i))-L\\ &=L-2\sum_{i=0}^L (\hat{x}_i\oplus\hat{y}_i)\qquad\text{XOR} \end{aligned}\]所以实际上二值神经网络并不是真的二值,仅仅是网络的权重采用二值表示,其余计算依然会涉及到整数及浮点数。
Conv
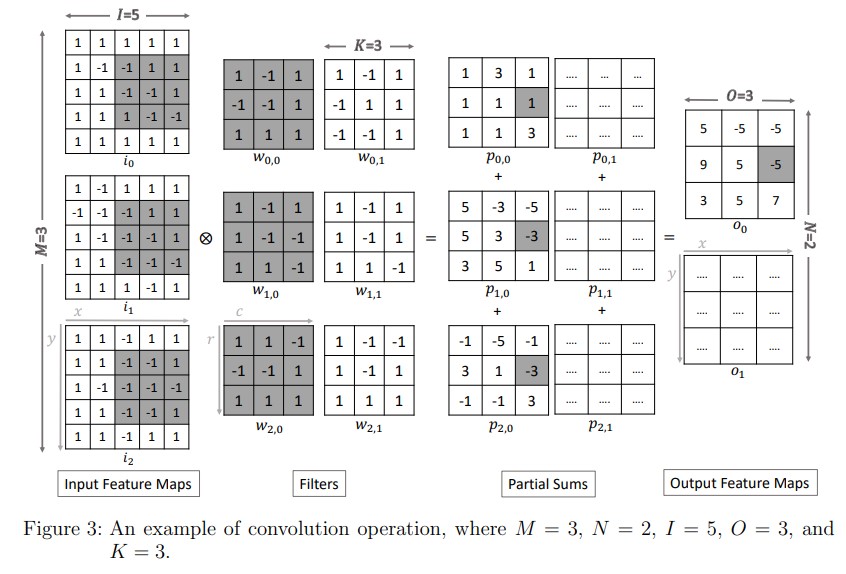
对应的有融合乘加(fused multiply-add, FMA)操作,这在CPU SIMD中很常见。
对于这种卷积操作,硬件可以很方便地通过XNOR和popcount实现,唯一改变是公式中的$L$变为kernel size。注意要进行bitpicking(通常pack channel),大位宽进行位运算会更加高效。
具体实现可参见packed_conv2d_nchw,下面的代码用HeteroCL编写。
batch, in_channel, in_height, in_width = Input.shape
num_filter, filter_channel, kernel_h, kernel_w = Filter.shape
rc = hcl.reduce_axis(0, in_channel, name=name+'_rc')
ry = hcl.reduce_axis(0, kernel_h, name=name+'_ry')
rx = hcl.reduce_axis(0, kernel_w, name=name+'_rx')
rb = hcl.reduce_axis(0, bitwidth, name=name+'_rb')
kernel_size = kernel_h * kernel_w
out = hcl.compute((batch, out_channel, out_height, out_width),
lambda nn, ff, yy, xx: kernel_size * bitwidth * in_channel -
(hcl.sum((Padded_Input[nn, rc_, yy * stride_h + ry, xx * stride_w + rx] ^ Filter[ff, rc_, ry, rx])[rb],
axis=[rc, ry, rx, rb], dtype=out_dtype, name=name) << 1),
name=name, dtype=out_dtype)
注意padding之后的元素并不算入popcount当中,因此在reduce求和之前需要先判断是否在padding的边界。
Max pooling
池化后的值大于0取1,否则取0。
Dense
同XNOR方式的矩阵乘,注意matmul的结果是有符号整数值,但bias是浮点数,故加完bias会变实数。
如果采用ReLU进行激活,则大于0归为1,否则归为0(二值)。
Batch norm
通常为了让神经网络不受批次影响,有更好的泛化能力,会采用类似CNN的Batch norm方法来做批归一化操作。
\[\mathbf{y}=\frac{\mathbf{x}-\mathbf{\mu}}{\sqrt{\sigma^2+\varepsilon}}\gamma+\beta\]归一化后做二值化,大于0取1,否则取0。
在具体实现这些层时一定要注意每一层的输出结果的类型,否则做量化时就会出错。
Popcount
BNN的conv2d和dense layer中最为核心的即为popcount的实现,这里会有很多magic methods,gcc (CPU)是提供了内置的intrinsic,但FPGA则需自己实现。可参考: