Hongzheng Chen Blog

CCC2021

Jun 10th, 2021  0

临近毕业没有事情干，就和同学参加了CCF体系结构专委举办的第一届定制算法挑战赛(Customized Computing Challenge, CCC’2021)。比赛形式是用Xilinx Vitis HLS（工具链组委会已经部署在云端）实现并优化一些算法的硬件电路，只需通过cosim模拟得到硬件的frequency和latency得到最终的性能指标，而无需实际上板，因此整个开发流程便捷了很多，大幅度降低了编程部署门槛。

初赛分为3个级别的题目，初级题包括经典的Sobel算子和FFT，中级题为排序、SVM、加密算法ECDSA，高级题为图算法（图直径、图染色、最小生成树）。其中，初级题2题必做，中级题3选2，高级题3选1，最后对三个级别的题目乘以难度系数后加权求和排名。

之前做研究的时候只是简单运用了HLS进行一些优化，一直没有深度应用过，这次比赛总算自己摸索出了HLS常用的优化方法以及面临的问题，虽然只差一点进入决赛（事实证明参加的队伍都非常强），但在这个过程中收获的技巧倒是大有裨益，因此本文还是对初赛的题目进行回顾，并给出我们的优化方法。

（本文持续更新中）

题目与规则

初赛题目可见OJ或Github。

性能公式为：

  • 如果最大频率小于100MHz，视为未通过基本功能
  • 如果最大频率大于等于100MHz，但小于300MHz，使用公式RTL simulation time/clock period/fmax计算性能
  • 如果最大频率大于等于300MHz，使用公式RTL simulation time/clock period/300MHz计算性能

其中RTL simulation time是Vitis HLS软件Cosimulation所用时间，clock period是tcl中设定的时钟频率，fmax是设计的最高运行频率。性能公式计算出的数值越小，性能越好。

因此，核心的优化目标是降低latency，同时保证最高运行频率fmax尽可能大。本赛题采用非常大的FPGA板，可以理解为不对资源进行限制。

Sobel（初级题）

概述

Sobel是数字图像处理中一个非常经典的算子/滤波器，用于提取图像边缘。原理是用离散梯度逼近连续的导数，计算时可以理解为一种卷积(conv)，意味着在深度学习领域有很多现成的硬件优化方法或许可以直接拿来使用。

其中x方向的卷积核为

\[G_x = \begin{bmatrix} -1 & 0 & 1\\ -2 & 0 & 2\\ -1 & 0 & 1 \end{bmatrix}\]

y方向的卷积核为

\[G_y = \begin{bmatrix} -1 & -2 & -1\\ 0 & 0 & 0\\ 1 & 2 & 1 \end{bmatrix}\]

由于卷积核非常简单，因此可以直接展开进行点积求和，每个卷积核只需进行6次乘加计算。

但本赛题规定 $G_x$ 和 $G_y$ 都必须为0-255之间的整数，最后总的梯度 $|G_x|+|G_y|$ 也需保证为0-255的整数，这使得两个卷积核没有办法直接融合在一起，而必须分开进行计算后再求和。

Baseline

根据上述描述可以非常快地写出软件实现代码如下，由于是2D滤波，因此循环也相对简单。

注意到输入的src和dst均为一维数组，因此需要先计算访问元素的地址，然后再读取数据计算。这里输入图像大小为1280*720，不需做padding。

#include "sobel.h"
#include <iostream>

inline PIXEL trunc(PIXEL res)
{
    if (res > 255)
        res = 255;
    else if (res < 0)
        res = 0;
    return res;
}

static PIXEL Gradient_X(PIXEL WB[3][3])
{
    PIXEL res;
    res = (WB[0][2] + (WB[1][2] << 1) + WB[2][2]) - (WB[0][0] + (WB[1][0] << 1) + WB[2][0]);
    return trunc(res);
}

static PIXEL Gradient_Y(PIXEL WB[3][3])
{
    PIXEL res;
    res = (WB[2][0] + (WB[2][1] << 1) + WB[2][2]) - (WB[0][0] + (WB[0][1] << 1) + WB[0][2]);
    return trunc(res);
}

static PIXEL sobel3x3_kernel(PIXEL WB[3][3])
{
    PIXEL gx = Gradient_X(WB);
    PIXEL gy = Gradient_Y(WB);
    PIXEL res = gx + gy;
    return trunc(res);
}

void sobel(PIXEL src[HEIGHT*WIDTH], PIXEL dst[(HEIGHT-2)*(WIDTH-2)], int rows, int cols)
{
    const int res_rows = HEIGHT-2;
    const int res_cols = WIDTH-2;
    for (int i = 0; i < res_rows; ++i)
        for (int j = 0; j < res_cols; ++j) {
            PIXEL WB[3][3];
            for (int ki = 0; ki < 3; ++ki)
                for (int kj = 0; kj < 3; ++kj)
                    WB[ki][kj] = src[(i+ki)*cols+j+kj];
            dst[i*res_cols+j] = sobel3x3_kernel(WB);
        }
}

基础优化-数据重用

卷积操作或者更一般的Stencil操作一个很大的问题在于其复杂的数据访问模式，其中存在大量的冗余数据访问。

比如一个3*3的2D卷积，每次向右平移一格（步长为1）后执行卷积操作，会存在6个重复元素的访问。（图片来源：HeteroCL Memory Customization）

为避免这些重复数据的大量访问，可以构建一个window buffer (WB)，专门用来实现数据重用(reuse)，即每次将WB里的数据往左移动一列，并添加新的一列数据进来。如果WB是用寄存器实现，而数据一开始存储在内存中，则每进行一次卷积操作，可以减少6次的内存访问（实际每次只需访问3次内存）。

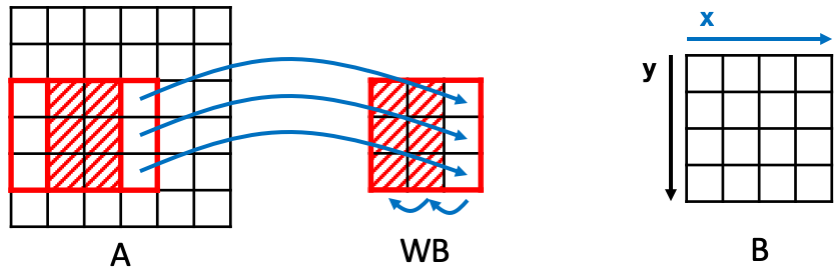
类似地，在行方向上也可实现数据重用。每次进行新一行的卷积操作时，上面两行的数据都是重复的，因此可以构建line buffer (LB)进行数据重用。每次将LB的数据上移一行，并读入新的一行进来。

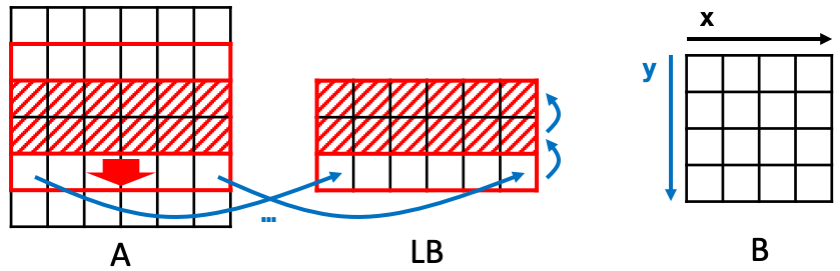
事实上，将上述两种重用模式进行结合，可以得到下图，即每次先读取LB中的数据，然后WB再从LB中进行读取，这样可以做到原图中的每个像素点都只用进行1次内存访问，且是从左到右从上到下顺序访问，这为流式架构(streaming architecture)的实现提供了可能性。

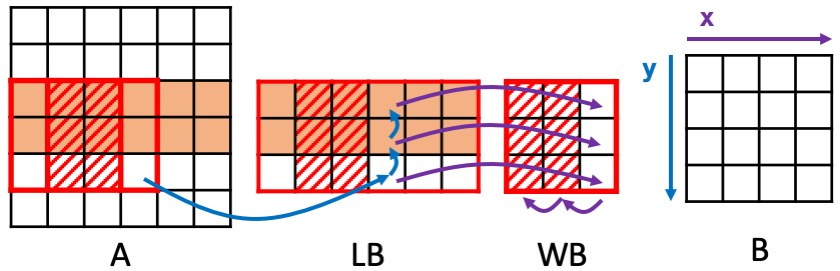
进而我们可以得到下面的实现。

void sobel(PIXEL src[HEIGHT*WIDTH], PIXEL dst[(HEIGHT-2)*(WIDTH-2)], int rows, int cols)
{
    const int res_rows = HEIGHT-2;
    const int res_cols = WIDTH-2;
    PIXEL LB[3][WIDTH];
    #pragma HLS array_partition variable=LB complete dim=1
    PIXEL WB[3][3];
    #pragma HLS array_partition variable=WB complete dim=0
    row:
    for (int i = 0; i < HEIGHT; ++i) {
        col:
        for (int j = 0; j < WIDTH; ++j) {
        #pragma HLS pipeline
            // move down line buffer
            // no dependency between different columns
            LB[0][j] = LB[1][j];
            LB[1][j] = LB[2][j];
            LB[2][j] = src[i*WIDTH+j];
            if (2 <= i) {
                // move right window buffer
                for (int lb_i = 0; lb_i < 3; ++lb_i) {
                    WB[lb_i][0] = WB[lb_i][1];
                    WB[lb_i][1] = WB[lb_i][2];
                    WB[lb_i][2] = LB[lb_i][j];
                }
                if (2 <= j) {
                    dst[(i-2)*res_cols+(j-2)] = sobel3x3_kernel(WB);
                }
            }
        }
    }
}

这里的HLS实现添加了几个pragma，首先在col层循环添加了pipeline，则里面所有的子循环都会被展开，即WB和LB的访问都是并行的，因此

  • LB的每一行都需要被分配到不同的memory bank（对应array_partition variable=LB complete dim=1），则LB[0]、LB[1]、LB[2]可以被同时写入，右侧的LB和src同样可以同时读取
  • WB一共9个元素的写入会被完全展开，故对应的存储也许完全展开（对应array_partition variable=WB complete dim=0），右侧LB涉及到3行的并行读取，在上一步已经进行划分
  • 关于src和dst，由于每轮循环只访问一次，故不需进行划分

注意到读操作一般需要至少2个时钟完成，第1个时钟读取地址，第2个时钟读取数据。而在存储体读取数据的时候就可以执行下一个数据地址读取的操作（此即pipeline的思想，重叠存储访问与计算），在流水线维度(j)上，都不存在内存冲突，即同一时刻同一memory bank只会收到一个读数据地址的请求，故循环的初始间隔(Initial interval, II)可以为1，即每隔1个时钟开启一个新的循环。

由于WB每一列的数据存在依赖关系（读后写，WAR），因此至少需要3+1个时钟（3列数据）完成数据移动及计算操作（组合逻辑latency视为0）。最后的latency可粗略估计为

latency = (Trip count - 1) * II + depth = (1280 * 720 - 1) * 1 + 4 = 921603

进阶优化-循环展开

上述是非常基础也非常标准的卷积优化方法，我们一曾以为这就是最优的，但当这题的排名从第一被刷到十几后，我们才发现其实哪怕是简单的卷积，优化的空间也还有很多。

要降低latency，从公式入手可以降低II和减少循环次数。而我们的II已经是1最优了，那就只能通过减少循环次数来达到latency的降低，也即增大并行度。

如同我们上述在comment中标注的，其实LB每次读取的列数据都是没有冲突的，因此可以一次性读入多列数据，来减少循环次数，这可以通过循环展开(unroll)实现。为了让计算也能够并行，可以创建局部的WB，每个WB都同时从LB中读取数据。虽然这会造成非常大的内存冲突，但是在后续实验中我们发现依然还是这种方式的性能最优。

void sobel(PIXEL src[HEIGHT*WIDTH], PIXEL dst[(HEIGHT-2)*(WIDTH-2)], int rows, int cols)
{
    const int res_rows = HEIGHT - 2;
    const int res_cols = WIDTH - 2;
    const int unroll_factor = 4;
    #pragma HLS array_partition variable=src cyclic factor=unroll_factor dim=0
    #pragma HLS array_partition variable=dst cyclic factor=unroll_factor dim=0
    PIXEL LB[3][WIDTH];
    #pragma HLS bind_storage variable=LB type=RAM_T2P impl=bram latency=1
    #pragma HLS bind_storage variable=LB type=RAM_T2P impl=bram latency=1
    #pragma HLS array_partition variable=LB complete dim=1
    #pragma HLS array_partition variable=LB cyclic factor=unroll_factor dim=2
    row:
    for (int i = 0; i < HEIGHT; ++i) {
        col:
        for (int j = 0; j < WIDTH; ++j) {
        #pragma HLS unroll factor=unroll_factor
        #pragma HLS pipeline
        #pragma HLS dependence variable=dst inter false
            // move down line buffer
            // no dependency between different columns
            LB[0][j] = LB[1][j];
            LB[1][j] = LB[2][j];
            LB[2][j] = src[i*WIDTH+j];
            if (2 <= i && 2 <= j) {
                PIXEL WB[3][3];
                #pragma HLS array_partition variable=WB complete dim=0
                line_buffer:
                for (int lb_i = 0; lb_i < 3; ++lb_i) {
                    WB[lb_i][0] = LB[lb_i][j-2];
                    WB[lb_i][1] = LB[lb_i][j-1];
                    WB[lb_i][2] = LB[lb_i][j];
                }
                dst[(i-2)*res_cols+(j-2)] = sobel3x3_kernel(WB);
            }
        }
    }
}

假设展开因子为4（并行度为4），则LB每次循环需要从src中读取4列数据（故src要以4为因子循环划分memory bank），同理向dst写入4列数据。

  • LB的读取不存在冲突，只是第二个维度同样需要以4为因子进行划分
  • 会同时存在4个局部WB，对LB中(4+2)*3=18个数据进行并行访问，其中还存在一列数据被3个WB同时请求的情况。考虑到一个BRAM最多有2个读/写端口，因此同个循环内响应3个WB的请求至少需要2个时钟进行地址传送，即II至少为2

通过HLS综合可以得到II=2，depth=8，则性能为

latency = (1280 * 720 / 4) * 2 + 8 = 460808

大约比原来提升了一倍。

但其实这种做法并不好，在cosim时会出现大量如下的冲突警告

14025NOTE:read & write conflict----port0 read and port1 write to the same address:00000 at the same clock. Write first Mode.

进阶优化-多PE处理

上述的做法验证了一定的可行性，但是由于内存冲突太严重，因此并没有办法做到进一步的性能提升。要进一步提升并行度，另外的思路则是采用多个处理单元(Processing Engine, PE)。

由于本问题不做padding，导致输出的feature map大小不是太好处理（1278*718），分解质因数为

  • 1278=2*3*3*71
  • 718=2*359

脉动阵列(Systolic Array, SA)

由于目前大部分的计算任务都是IO bound的，即与内存通信占据了整个计算流程的大部分时间，而脉动阵列的思想很简单，即在尽可能提升并行度的同时，让数据在片上流动得久一些。数据从内存读入后经过大量的处理单元后再流出，从而减少内存访问次数，脉动阵列也成为目前TPU的核心硬件架构。

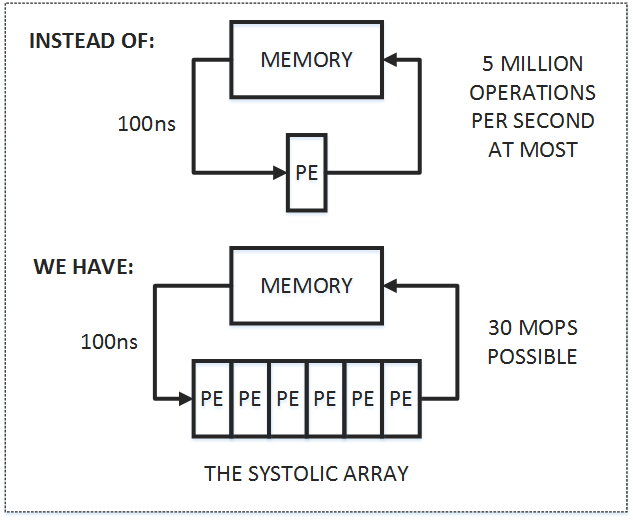
一个3*3的矩阵乘SA计算流程如下（摘自AutoSA文档），可以看到只需5个时钟即可完成读入与计算，所有的数据传输都采用数据流(streaming)。

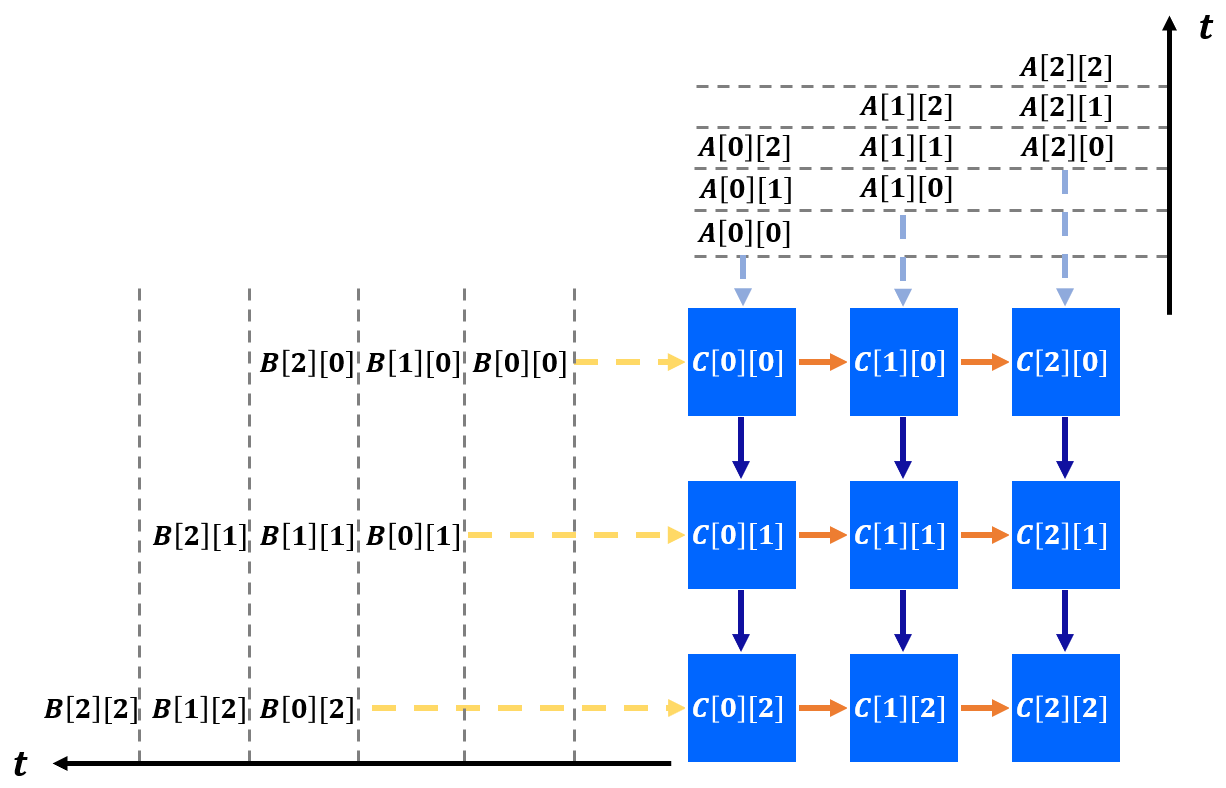
类似的，卷积操作也可以采用这种架构，从而实现硬件加速。

由于脉动阵列手写非常麻烦，我们采用AutoSA来进行自动生成，可见这份Tutorial（更多关于脉动阵列的内容可见FCCM’21的Workshop）。

又由于SA的大小必须是输出矩阵大小的因子，故可以选择的结构并不是很多。我们生成了2*9大小的SA，一个SA用于计算一个方向上的卷积，用两个SA分别计算$G_x$和$G_y$，最后输出结果通过trunc再最后叠加。代码如下所示，kernel0为生成的SA入口函数。

void accumulate(PIXEL dst[HEIGHT * WIDTH], PIXEL dst1[(HEIGHT - 2) * (WIDTH - 2)], PIXEL dst2[(HEIGHT - 2) * (WIDTH - 2)])
{
  const int res_rows = HEIGHT - 2;
  const int res_cols = WIDTH - 2;
    for (int i = 0; i < res_rows * res_cols; ++i) {
  #pragma HLS pipeline
    PIXEL res = dst1[i] + dst2[i];
    dst[i] = trunc(res);
  }
}

void sobel(PIXEL src[HEIGHT * WIDTH], PIXEL dst[(HEIGHT - 2) * (WIDTH - 2)], int rows, int cols)
{
#pragma HLS interface ap_ctrl_chain port=return
#pragma HLS dataflow
  PIXEL w1[9] = {-1, 0, 1, -2, 0, 2, -1, 0, 1};
  PIXEL dst1[(HEIGHT - 2) * (WIDTH - 2)];
  kernel0(src, dst1, w1);
  PIXEL w2[9] = {-1, -2, -1, 0, 0, 0, 1, 2, 1};
  PIXEL dst2[(HEIGHT - 2) * (WIDTH - 2)];
  kernel0(src, dst2, w2);
  accumulate(dst, dst1, dst2);
}

但实际综合出来的结果并不好，远没有18的并行度，结果是到了1086620 cycles。当时没有去深究原因，但似乎是自动生成的PE实现（764681）、PE间通信（CIN_IO_L2 931399）都还未达到最优。

分块(Tiling)

注意到输入矩阵每一部分的卷积实际上都没有依赖，可以并行地做，因此就可以将输入矩阵划分为多块，然后分别进行kernel计算，再输出至对应的格中。但对于卷积来说，一个比较麻烦的问题是边界的处理，其不像矩阵乘，只会访问到划分块内的元素。假设输出块的大小为x*y，则输入块的大小为(x+2)*(y+2)，意味着相邻块之间存在重叠。

为了保证每个PE计算量的均衡，我们可以从输出矩阵大小入手进行等量划分。比如划分成2*2块，那么每块大小就是(718/2)*(1278/2)，而输入块的大小是(359+2)*(639+2)，可以得到下面的代码，全部都使用FIFO (hls::stream)进行传输。由于顶层函数签名src和dst都不是stream变量，因此需要另外创建读写进程read_proc和write_proc。

const int TILE_HI = 361;
const int TILE_WI = 641;
const int TILE_HO = 359;
const int TILE_WO = 639;

template<int start_row, int end_row, int start_col, int end_col>
void tile_sobel(hls::stream<PIXEL>& src, hls::stream<PIXEL>& dst) {
  const int res_cols = WIDTH - 2;
  PIXEL LB[3][TILE_WI];
#pragma HLS array_partition variable = LB complete dim = 1
  PIXEL WB[3][3];
#pragma HLS array_partition variable = WB complete dim = 0
  for (int i = start_row; i < end_row; ++i)
  {
    for (int j = start_col; j < end_col; ++j)
    {
#pragma HLS pipeline
#pragma HLS dependence variable = dst inter false
      // move down line buffer
      // no dependency between different columns
      int lb_j = j - start_col;
      LB[0][lb_j] = LB[1][lb_j];
      LB[1][lb_j] = LB[2][lb_j];
      LB[2][lb_j] = src.read();
      if (start_row+2 <= i)
      {
        // move right window buffer
        for (int lb_i = 0; lb_i < 3; ++lb_i)
        {
          WB[lb_i][0] = WB[lb_i][1];
          WB[lb_i][1] = WB[lb_i][2];
          WB[lb_i][2] = LB[lb_i][lb_j];
        }
        if (start_col+2 <= j)
        {
          dst.write(sobel3x3_kernel(WB));
        }
      }
    }
  }
}

void read_proc(PIXEL src[HEIGHT * WIDTH], hls::stream<PIXEL>& s_src0, hls::stream<PIXEL>& s_src1, hls::stream<PIXEL>& s_src2, hls::stream<PIXEL>& s_src3)
{
  for (int i = 0; i < TILE_HI; ++i) {
    for (int j = 0; j < TILE_WI; ++j)
    {
      #pragma HLS pipeline
      PIXEL tmp0 = src[(i + 0) * WIDTH + j + 0];
      s_src0.write(tmp0);
      PIXEL tmp1 = src[(i + 0) * WIDTH + j + 639];
      s_src1.write(tmp1);
      PIXEL tmp2 = src[(i + 359) * WIDTH + j + 0];
      s_src2.write(tmp2);
      PIXEL tmp3 = src[(i + 359) * WIDTH + j + 639];
      s_src3.write(tmp3);
    }
  }
}

void write_proc(PIXEL dst[(HEIGHT-2) * (WIDTH-2)], hls::stream<PIXEL>& s_dst0, hls::stream<PIXEL>& s_dst1, hls::stream<PIXEL>& s_dst2, hls::stream<PIXEL>& s_dst3)
{
  #pragma HLS DEPENDENCE variable=dst intra WAW false
  for (int i = 0; i < TILE_HO; ++i) {
    for (int j = 0; j < TILE_WO; ++j)
    {
      #pragma HLS pipeline
      dst[(i + 0) * (WIDTH-2) + j + 0] = s_dst0.read();
      dst[(i + 0) * (WIDTH-2) + j + 639] = s_dst1.read();
      dst[(i + 359) * (WIDTH-2) + j + 0] = s_dst2.read();
      dst[(i + 359) * (WIDTH-2) + j + 639] = s_dst3.read();
    }
  }
}

void sobel(PIXEL src[HEIGHT*WIDTH], PIXEL dst[(HEIGHT-2)*(WIDTH-2)], int rows, int cols)
{
#pragma HLS interface ap_ctrl_chain port=return
#pragma HLS dataflow
    #pragma HLS array_partition variable=src cyclic factor=18 dim=1
    #pragma HLS array_partition variable=dst cyclic factor=18 dim=1
    hls::stream<PIXEL> s_src0, s_dst0;
    #pragma HLS STREAM variable=s_src0 depth=TILE_HI*TILE_WI
    #pragma HLS STREAM variable=s_dst0 depth=TILE_HI*TILE_WI
    hls::stream<PIXEL> s_src1, s_dst1;
    #pragma HLS STREAM variable=s_src1 depth=TILE_HI*TILE_WI
    #pragma HLS STREAM variable=s_dst1 depth=TILE_HI*TILE_WI
    hls::stream<PIXEL> s_src2, s_dst2;
    #pragma HLS STREAM variable=s_src2 depth=TILE_HI*TILE_WI
    #pragma HLS STREAM variable=s_dst2 depth=TILE_HI*TILE_WI
    hls::stream<PIXEL> s_src3, s_dst3;
    #pragma HLS STREAM variable=s_src3 depth=TILE_HI*TILE_WI
    #pragma HLS STREAM variable=s_dst3 depth=TILE_HI*TILE_WI
    read_proc(src, s_src0, s_src1, s_src2, s_src3);
    tile_sobel<0, 361, 0, 641>(s_src0, s_dst0);
    tile_sobel<0, 361, 639, 1280>(s_src1, s_dst1);
    tile_sobel<359, 720, 0, 641>(s_src2, s_dst2);
    tile_sobel<359, 720, 639, 1280>(s_src3, s_dst3);
    write_proc(dst, s_dst0, s_dst1, s_dst2, s_dst3);
}

由于上述代码非常规整，因此我们另外用Python编写了代码生成器，用于上述tiling的边界计算和生成。

看上去这种tiling采用了4个PE同时进行计算应该可以达到4倍的并行度，但实际上由于存在重叠部分，在数据读取和写入时并没有办法做到并行（src和dst数组无论划分的factor为多少，都会产生内存访问冲突），最终导致读写进程的II不为1，综合出来的结果也不佳。

其他优化思路

对于通用卷积来说，已经有了大量成熟的加速方法，包括im2col和Winograd，但是将它们部署在FPGA上都面临着一定的问题。

im2col

现在深度学习框架中常用的加速卷积的方法是im2col+GEMM，核心思想是将卷积计算的窗口重新组织成矩阵的形式，然后就可以调用通用的矩阵运算库进行加速。

如考虑下面3*4大小的输入特征，卷积核大小为3*3，那么输出特征大小为1*2。

\[\begin{bmatrix} a_{00} & a_{01} & a_{02} & a_{03}\\ a_{10} & a_{11} & a_{12} & a_{13}\\ a_{20} & a_{21} & a_{22} & a_{23}\\ \end{bmatrix}\]

可以将卷积计算过程改写为下列矩阵乘的形式，其中卷积核展平为1*9的向量，卷积窗口展为9*2的矩阵，进而可以使用GEMM进行计算。（注意最后是需要通过col2img进行恢复的，因为输出只有一行）

\[\begin{bmatrix} k_{00} & k_{01} & k_{02} & k_{10} & k_{11} & k_{12} & k_{20} & k_{21} & k_{22} \end{bmatrix} \cdot \begin{bmatrix} a_{00} & a_{01}\\ a_{01} & a_{02}\\ a_{02} & a_{03}\\ a_{10} & a_{11}\\ a_{11} & a_{12}\\ a_{12} & a_{13}\\ a_{20} & a_{21}\\ a_{21} & a_{22}\\ a_{22} & a_{23} \end{bmatrix}\]

这种方法虽然充分利用到了现有的矩阵加速库，但是其转换步骤依然非常耗时。翻阅了不少文献，发现都没有针对im2col这一步骤的优化加速。尽管实际计算是加速了，但是数据读取一侧依然没有提速的话（依然需要O(M*N)数据读取的复杂度/循环次数），那对于整体加速收益其实是不够的。

另外一种可能性是im2col这一步操作可以当作是预处理，在CPU上完成，当数据组织好后再送入加速卡（GPU/FPGA）进行加速，这也许是通用做法，但并不符合本次比赛的要求。

Winograd

Winograd也是一种常用的优化卷积的算法，最早被运用在FIR滤波器上，后来于2015年重新被人挖掘运用在深度学习上（参见这篇论文）。

主要思想是通过代数变换，从而减少乘法次数。但是同样对于FPGA来说，对于本问题的卷积核都为整数，winograd可能并不会起到太大作用，最多减少单个循环的latency（即depth），但是不会影响循环次数，进而无法提升最终性能。

FFT（初级题）

概述

快速傅里叶变换(Fast Fourier Transformation, FFT)是信号处理的基石，在不同场景中都有广泛的应用。

\[F(k)=\sum _{n=0}^{N-1}f(k)e^{-\frac{2\pi}{N} ikn}\qquad k=0,\ldots ,N-1\]

考虑将上面的式子进行奇偶分拆（0,2,4,6一组，1,3,5,7一组），可以得到（令$f_1(r):=f(2r),f_2(r):=f(2r+1)$）

\[\begin{aligned} F(k)&=\sum_{r=0}^{N/2-1}f(2r)e^{-\frac{2\pi}{N} ik2r} + \sum_{r=0}^{N/2-1}f(2r+1)e^{-\frac{2\pi}{N} ik(2r+1)}\\ &=\sum_{r=0}^{N/2-1}f_1(r)e^{-\frac{2\pi}{N/2} ikr} + \sum_{r=0}^{N/2-1}f_2(r)e^{-\frac{2\pi}{N/2} ikr}\cdot e^{-\frac{2\pi}{N}ik}\\ &=F_1^{N/2}(k)+\overline{\omega_N^k} F_2^{N/2}(k),\qquad k=0,\ldots,N/2-1 \end{aligned}\]

类似地，可以导出后一半的计算公式

\[F(k+N/2)=F_1^{N/2}(k)-\overline{\omega_N^k} F_2^{N/2}(k),\qquad k=0,\ldots,N/2-1\]

其中$\overline{\omega_N^k}$为第$k$个$N$次单位根的共轭。也就是说原来的FFT可以被拆解为两个小的FFT分别计算，然后再合并。

类似的思想可以递归下去，直至只有两个元素，那么就变成了基本的蝶形变换。之所以叫蝶形变换，正是因为其每次计算时取两个元素进行交叉乘加。这种计算方式也即大名鼎鼎的Cooley-Tukey算法，计算过程如下图所示。

注意到最开始的数组下标并不是规整的，这正是每次奇偶分组后得到的结果。

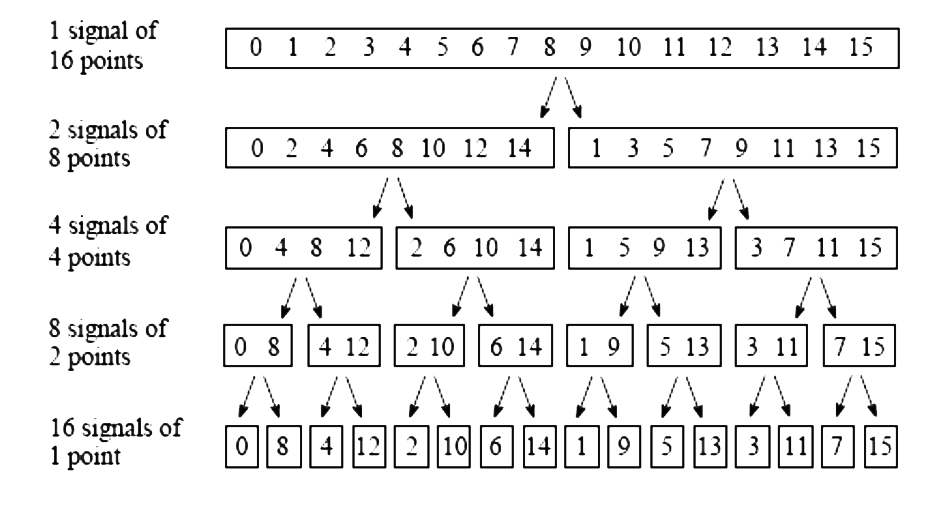
如果正向进行计算，则在最开始需要进行位反转(bit reverse)操作，将对应数组元素进行交换后，再进行$\log n$次的蝶形计算（如$N=1024$需要进行10个stage的蝶形求值）。

Baseline

有了上述分析后，可以很快写出对应的FFT代码。为了代码结构的简介，这里最开始参照了这份代码进行编写，并拆开实部X_R和虚部X_I。本题的SIZE为1024，DTYPE为float。

这里比较奢侈地每个stage都新开了数组存储中间结果，尽可能减少相邻stage的内存访问冲突。而cos和sin的系数都已经提前计算好常数表方便直接读取，因此代码中只需通过W_real和W_imag进行访问即可。（W_real[k]=cos(-2*PI*k/SIZE);）

具体到每个stage，每个输入的FFT组大小是$2^s$，共有$2^{10-s}$个组。设$F_1=R_1+iI_1$，$F_2=R_2+iI_2$，$\theta=-\frac{2\pi}{N}k$，则

\[\begin{aligned} F(k)&=R_1+(R_2\cos\theta-I_2\sin\theta)\\ &+i(I_1+(I_2\cos\theta +R_2\sin\theta))\\ F(k+N/2)&=R_1-(R_2\cos\theta-I_2\sin\theta)\\ &+i(I_1-(I_2\cos\theta +R_2\sin\theta))\\ \end{aligned}\]

对应地可以写出以下代码，内层循环遍历每一个组，外层循环遍历组内的元素（循环次数为组大小/2）。

#include "fft.h"

void bit_reverse(DTYPE X_R[SIZE], DTYPE X_I[SIZE], DTYPE OUT_R[SIZE], DTYPE OUT_I[SIZE]);
void fft_stage_first(DTYPE X_R[SIZE], DTYPE X_I[SIZE], DTYPE OUT_R[SIZE], DTYPE OUT_I[SIZE]);
void fft_stages(DTYPE X_R[SIZE], DTYPE X_I[SIZE], int STAGES, DTYPE OUT_R[SIZE], DTYPE OUT_I[SIZE]);
void fft_stage_last(DTYPE X_R[SIZE], DTYPE X_I[SIZE], DTYPE OUT_R[SIZE], DTYPE OUT_I[SIZE]);


void fft(DTYPE X_R[SIZE], DTYPE X_I[SIZE], DTYPE OUT_R[SIZE], DTYPE OUT_I[SIZE])
{
#pragma HLS dataflow

  //Call fft
  DTYPE Stage1_R[SIZE], Stage1_I[SIZE];
  DTYPE Stage2_R[SIZE], Stage2_I[SIZE];
  DTYPE Stage3_R[SIZE], Stage3_I[SIZE];
  DTYPE Stage4_R[SIZE], Stage4_I[SIZE];
  DTYPE Stage5_R[SIZE], Stage5_I[SIZE];
  DTYPE Stage6_R[SIZE], Stage6_I[SIZE];
  DTYPE Stage7_R[SIZE], Stage7_I[SIZE];
  DTYPE Stage8_R[SIZE], Stage8_I[SIZE];
  DTYPE Stage9_R[SIZE], Stage9_I[SIZE];
  DTYPE Stage10_R[SIZE], Stage10_I[SIZE];

  bit_reverse(X_R, X_I, Stage1_R, Stage1_I);
  fft_stage_first(Stage1_R, Stage1_I, Stage2_R, Stage2_I);
  fft_stages(Stage2_R, Stage2_I, 2, Stage3_R, Stage3_I);
  fft_stages(Stage3_R, Stage3_I, 3, Stage4_R, Stage4_I);
  fft_stages(Stage4_R, Stage4_I, 4, Stage5_R, Stage5_I);
  fft_stages(Stage5_R, Stage5_I, 5, Stage6_R, Stage6_I);
  fft_stages(Stage6_R, Stage6_I, 6, Stage7_R, Stage7_I);
  fft_stages(Stage7_R, Stage7_I, 7, Stage8_R, Stage8_I);
  fft_stages(Stage8_R, Stage8_I, 8, Stage9_R, Stage9_I);
  fft_stages(Stage9_R, Stage9_I, 9, Stage10_R, Stage10_I);
  fft_stage_last(Stage10_R, Stage10_I, OUT_R, OUT_I);

}

unsigned int reverse_bits(unsigned int input) {
  int i, rev = 0;
  for (i = 0; i < M; i++) {
    rev = (rev << 1) | (input & 1);
    input = input >> 1;
  }
  return rev;
}

void bit_reverse(DTYPE X_R[SIZE], DTYPE X_I[SIZE], DTYPE OUT_R[SIZE], DTYPE OUT_I[SIZE]) {
  //Insert your code here
  unsigned int reversed;
  unsigned int i;

  for (int i = 0; i < SIZE; i++) {
  #pragma HLS pipeline
      reversed = reverse_bits(i); // Find the bit reversed index
    if (i <= reversed) {
      // Swap the real values
      OUT_R[i] = X_R[reversed];
      OUT_R[reversed] = X_R[i];

      // Swap the imaginary values
      OUT_I[i] = X_I[reversed];
      OUT_I[reversed] = X_I[i];
    }
  }
}

//stage 1
void fft_stage_first(DTYPE X_R[SIZE], DTYPE X_I[SIZE], DTYPE OUT_R[SIZE], DTYPE OUT_I[SIZE]) {
//Insert your code here
  int DFTpts = 1 << 1;    // DFT = 2^stage = points in sub DFT
  int numBF = DFTpts / 2;     // Butterfly WIDTHS in sub-DFT
  int step = SIZE >> 1;
  // Perform butterflies for j-th stage
  butterfly_loop:
  for (int j = 0; j < numBF; j++) {
  #pragma HLS loop_tripcount min=1 max=1 avg=1
    DTYPE c = W_real[j<<9];
    DTYPE s = W_imag[j<<9];
    dft_loop:
    for (int i = j; i < SIZE; i += DFTpts) { // 2
    #pragma HLS pipeline
    #pragma HLS loop_tripcount min=512 max=512 avg=512
      int i_lower = i + numBF; // index of lower point in butterfly
      // i: 0, 2, 4, ...
      // i_lower: 1, 3, 5, ...
      DTYPE temp_R = X_R[i_lower] * c - X_I[i_lower] * s;
      DTYPE temp_I = X_I[i_lower] * c + X_R[i_lower] * s;
      OUT_R[i_lower] = X_R[i] - temp_R;
      OUT_I[i_lower] = X_I[i] - temp_I;
      OUT_R[i] = X_R[i] + temp_R;
      OUT_I[i] = X_I[i] + temp_I;
    }
  }
}

//stages
void fft_stages(DTYPE X_R[SIZE], DTYPE X_I[SIZE], int stage, DTYPE OUT_R[SIZE], DTYPE OUT_I[SIZE]) {
//Insert your code here
  int DFTpts = 1 << stage;    // DFT = 2^stage = points in sub DFT
  int numBF = DFTpts / 2;     // Butterfly WIDTHS in sub-DFT
  int step = SIZE >> 2;
  // Perform butterflies for j-th stage
  butterfly_loop:
  for (int j = 0; j < numBF; j++) {
  #pragma HLS loop_tripcount min=256 max=256 avg=256
    DTYPE c = W_real[j<<(10-stage)];
    DTYPE s = W_imag[j<<(10-stage)];
    dft_loop:
    for (int i = j; i < SIZE; i += DFTpts) {
    #pragma HLS pipeline
    #pragma HLS loop_tripcount min=256 max=256 avg=256
      int i_lower = i + numBF; // index of lower point in butterfly
      DTYPE temp_R = X_R[i_lower] * c - X_I[i_lower] * s;
      DTYPE temp_I = X_I[i_lower] * c + X_R[i_lower] * s;
      OUT_R[i_lower] = X_R[i] - temp_R;
      OUT_I[i_lower] = X_I[i] - temp_I;
      OUT_R[i] = X_R[i] + temp_R;
      OUT_I[i] = X_I[i] + temp_I;
    }
  }
}

//last stage
void fft_stage_last(DTYPE X_R[SIZE], DTYPE X_I[SIZE], DTYPE OUT_R[SIZE], DTYPE OUT_I[SIZE]) {
//Insert your code here
  int DFTpts = 1 << 10;    // DFT = 2^stage = points in sub DFT
  int numBF = DFTpts / 2;     // Butterfly WIDTHS in sub-DFT
  int step = SIZE >> 10;
  // Perform butterflies for j-th stage
  butterfly_loop:
  for (int j = 0; j < numBF; j++) {
  #pragma HLS loop_tripcount min=512 max=512 avg=512
    DTYPE c = W_real[j];
    DTYPE s = W_imag[j];
    dft_loop:
    for (int i = j; i < SIZE; i += DFTpts) {
    #pragma HLS pipeline
    #pragma HLS loop_tripcount min=1 max=1 avg=1
      int i_lower = i + numBF; // index of lower point in butterfly
      DTYPE temp_R = X_R[i_lower] * c - X_I[i_lower] * s;
      DTYPE temp_I = X_I[i_lower] * c + X_R[i_lower] * s;
      OUT_R[i_lower] = X_R[i] - temp_R;
      OUT_I[i_lower] = X_I[i] - temp_I;
      OUT_R[i] = X_R[i] + temp_R;
      OUT_I[i] = X_I[i] + temp_I;
    }
  }
}

下面粗略计算总的latency。首先是bit_reverse，由于HLS无法判定i和reversed是否会写同一个位置，因此存在写后写的依赖，该循环II=2，进而latency为(1024-1)*2+3=2049（假设读后写需要3个周期）。

对于下面的stage，由于只在里层循环做pipeline，外层循环会被flatten入内层循环（当然上述代码结构可能不会出发自动flatten，因为c和s在两层循环中间，导致其非规则完美循环），因此总的循环次数都为512，由于每次数组读写的位置均不同，故II可以达到1，进而每个stage的latency为(512-1)*1+3=514。

综合最终的性能为（注意浮点数乘加计算的latency可能远超3个周期）

latency=2049+514*10=7189

基础优化-代码重构

上面的基线程序循环都达到II=1了，似乎已经没有什么可以优化的了，但事实上并不是这样的。

pipeline仅仅实现了流水线，但是并没有最大程度利用硬件片上拥有的资源。通过循环unroll可以进一步增大并行性，减少循环次数，从而减少最终的latency。

下面的代码进行了一定重构，并做了几点优化：

  1. 使用template实现fft_stages，这样可以在编译时就将stage编号作为常量输入，方便pragma的编写
  2. bit_reverse函数对i和reversed的地址进行分类讨论，避免读写同一地址的情况发生，同时显式告知HLS写后写(WAW)的依赖是不存在的，进而该循环可以做到II=1
  3. 将fft_stage_first和fft_stage_last缩减为一个循环，因为有一层循环的循环次数为1
  4. 将dft_loop的循环起始设置为0~loop_times，在编译时即可确定循环次数，方便HLS给出性能结果
  5. 对dft_loop中读取X_R和X_I的操作，创建局部变量进行存储，避免在下面计算时再重复读取
  6. 对dft_loop进行unroll操作，同时对应的输入输出数组也进行cyclic的划分
void bit_reverse(DTYPE X_R[SIZE], DTYPE X_I[SIZE], DTYPE OUT_R[SIZE], DTYPE OUT_I[SIZE]);
void fft_stage_first(DTYPE X_R[SIZE], DTYPE X_I[SIZE], DTYPE OUT_R[SIZE], DTYPE OUT_I[SIZE]);

template<int stage>
void fft_stages(DTYPE X_R[SIZE], DTYPE X_I[SIZE], DTYPE OUT_R[SIZE], DTYPE OUT_I[SIZE]);

void fft_stage_last(DTYPE X_R[SIZE], DTYPE X_I[SIZE], DTYPE OUT_R[SIZE], DTYPE OUT_I[SIZE]);


void fft(DTYPE X_R[SIZE], DTYPE X_I[SIZE], DTYPE OUT_R[SIZE], DTYPE OUT_I[SIZE])
{
#pragma HLS interface ap_ctrl_chain port=return
#pragma HLS dataflow

  DTYPE Stage1_R[SIZE], Stage1_I[SIZE];
  #pragma HLS array_partition variable=Stage1_R cyclic factor=16 dim=1
  #pragma HLS array_partition variable=Stage1_I cyclic factor=16 dim=1
  DTYPE Stage2_R[SIZE], Stage2_I[SIZE];
  #pragma HLS array_partition variable=Stage2_R cyclic factor=16 dim=1
  #pragma HLS array_partition variable=Stage2_I cyclic factor=16 dim=1
  DTYPE Stage3_R[SIZE], Stage3_I[SIZE];
  #pragma HLS array_partition variable=Stage3_R cyclic factor=8 dim=1
  #pragma HLS array_partition variable=Stage3_I cyclic factor=8 dim=1
  DTYPE Stage4_R[SIZE], Stage4_I[SIZE];
  #pragma HLS array_partition variable=Stage4_R cyclic factor=8 dim=1
  #pragma HLS array_partition variable=Stage4_I cyclic factor=8 dim=1
  DTYPE Stage5_R[SIZE], Stage5_I[SIZE];
  #pragma HLS array_partition variable=Stage5_R cyclic factor=8 dim=1
  #pragma HLS array_partition variable=Stage5_I cyclic factor=8 dim=1
  DTYPE Stage6_R[SIZE], Stage6_I[SIZE];
  #pragma HLS array_partition variable=Stage6_R cyclic factor=8 dim=1
  #pragma HLS array_partition variable=Stage6_I cyclic factor=8 dim=1
  DTYPE Stage7_R[SIZE], Stage7_I[SIZE];
  #pragma HLS array_partition variable=Stage7_R cyclic factor=8 dim=1
  #pragma HLS array_partition variable=Stage7_I cyclic factor=8 dim=1
  DTYPE Stage8_R[SIZE], Stage8_I[SIZE];
  #pragma HLS array_partition variable=Stage8_R cyclic factor=8 dim=1
  #pragma HLS array_partition variable=Stage8_I cyclic factor=8 dim=1
  DTYPE Stage9_R[SIZE], Stage9_I[SIZE];
  #pragma HLS array_partition variable=Stage9_R cyclic factor=8 dim=1
  #pragma HLS array_partition variable=Stage9_I cyclic factor=8 dim=1
  DTYPE Stage10_R[SIZE], Stage10_I[SIZE];
  #pragma HLS array_partition variable=Stage10_R cyclic factor=8 dim=1
  #pragma HLS array_partition variable=Stage10_I cyclic factor=8 dim=1
  #pragma HLS array_partition variable=OUT_R cyclic factor=8 dim=1
  #pragma HLS array_partition variable=OUT_I cyclic factor=8 dim=1
  bit_reverse(X_R, X_I, Stage1_R, Stage1_I);
  fft_stage_first(Stage1_R, Stage1_I, Stage2_R, Stage2_I);
  fft_stages<2>(Stage2_R, Stage2_I, Stage3_R, Stage3_I);
  fft_stages<3>(Stage3_R, Stage3_I, Stage4_R, Stage4_I);
  fft_stages<4>(Stage4_R, Stage4_I, Stage5_R, Stage5_I);
  fft_stages<5>(Stage5_R, Stage5_I, Stage6_R, Stage6_I);
  fft_stages<6>(Stage6_R, Stage6_I, Stage7_R, Stage7_I);
  fft_stages<7>(Stage7_R, Stage7_I, Stage8_R, Stage8_I);
  fft_stages<8>(Stage8_R, Stage8_I, Stage9_R, Stage9_I);
  fft_stages<9>(Stage9_R, Stage9_I, Stage10_R, Stage10_I);
  fft_stage_last(Stage10_R, Stage10_I, OUT_R, OUT_I);
}

unsigned int reverse_bits(unsigned int input) {
  int i, rev = 0;
  for (i = 0; i < M; i++) {
    rev = (rev << 1) | (input & 1);
    input = input >> 1;
  }
  return rev;
}

void bit_reverse(DTYPE X_R[SIZE], DTYPE X_I[SIZE], DTYPE OUT_R[SIZE], DTYPE OUT_I[SIZE]) {
  //Insert your code here
  unsigned int reversed;
  unsigned int i;

  #pragma HLS DEPENDENCE variable=OUT_I intra WAW false
  #pragma HLS DEPENDENCE variable=OUT_R intra WAW false
  for (int i = 0; i < SIZE; i++) {
  #pragma HLS pipeline
      reversed = reverse_bits(i); // Find the bit reversed index
    if (i < reversed) {
      // Swap the real values
      OUT_R[i] = X_R[reversed];
      OUT_R[reversed] = X_R[i];

      // Swap the imaginary values
      OUT_I[i] = X_I[reversed];
      OUT_I[reversed] = X_I[i];
    } else if (i == reversed) {
      // Swap the real values
      OUT_R[i] = X_R[reversed];

      // Swap the imaginary values
      OUT_I[i] = X_I[reversed];
    }
  }
}

//stage 1
void fft_stage_first(DTYPE X_R[SIZE], DTYPE X_I[SIZE], DTYPE OUT_R[SIZE], DTYPE OUT_I[SIZE]) {
//Insert your code here
  int DFTpts = 1 << 1;    // DFT = 2^stage = points in sub DFT
  int numBF = DFTpts / 2;     // Butterfly WIDTHS in sub-DFT
  DTYPE c = W_real[0<<9];
  DTYPE s = W_imag[0<<9];
  // Compute butterflies that use same W**k
  dft_loop:
  for (int i = 0; i < SIZE; i += DFTpts) {
  #pragma HLS unroll factor=8
    int i_lower = i + numBF; // index of lower point in butterfly
    // i: 0, 2, 4, ...
    // i_lower: 1, 3, 5, ...
    DTYPE xr_lower = X_R[i_lower];
    DTYPE xi_lower = X_I[i_lower];
    DTYPE temp_R = xr_lower * c - xi_lower * s;
    DTYPE temp_I = xi_lower * c + xr_lower * s;
    DTYPE xr = X_R[i];
    DTYPE xi = X_I[i];
    OUT_R[i_lower] = xr - temp_R;
    OUT_I[i_lower] = xi - temp_I;
    OUT_R[i] = xr + temp_R;
    OUT_I[i] = xi + temp_I;
  }
}

template<int stage>
void fft_stages(DTYPE X_R[SIZE], DTYPE X_I[SIZE], DTYPE OUT_R[SIZE], DTYPE OUT_I[SIZE]) {
//Insert your code here
  // stage 2-9
  const int DFTpts = 1 << stage;    // DFT = 2^stage = points in sub DFT
  // 4-512
  const int numBF = DFTpts / 2;     // Butterfly WIDTHS in sub-DFT
  const int loop_times = SIZE / DFTpts;
  // 2-256
  // Perform butterflies for j-th stage
  butterfly_loop:
  for (int j = 0; j < numBF; j++) {
    DTYPE c = W_real[j << (10 - stage)];
    DTYPE s = W_imag[j << (10 - stage)];
    // Compute butterflies that use same W**k
    // i and i_lower in all the loops are never the same,
    // covering 0-1024 all the elements when enumerating j
    dft_loop:
    for (int i_tmp = 0; i_tmp < loop_times; ++i_tmp) {
    #pragma HLS unroll factor=8
      int i = i_tmp * DFTpts + j;
      int i_lower = i + numBF; // index of lower point in butterfly
      DTYPE xr_lower = X_R[i_lower];
      DTYPE xi_lower = X_I[i_lower];
      DTYPE temp_R = xr_lower * c - xi_lower * s;
      DTYPE temp_I = xi_lower * c + xr_lower * s;
      DTYPE xr = X_R[i];
      DTYPE xi = X_I[i];
      OUT_R[i_lower] = xr - temp_R;
      OUT_I[i_lower] = xi - temp_I;
      OUT_R[i] = xr + temp_R;
      OUT_I[i] = xi + temp_I;
    }
  }
}

//last stage
void fft_stage_last(DTYPE X_R[SIZE], DTYPE X_I[SIZE], DTYPE OUT_R[SIZE], DTYPE OUT_I[SIZE]) {
//Insert your code here
  int DFTpts = 1 << 10;    // DFT = 2^stage = points in sub DFT
  int numBF = DFTpts / 2;     // Butterfly WIDTHS in sub-DFT
  // Perform butterflies for j-th stage
  butterfly_loop:
  for (int j = 0; j < numBF; j++) {
  #pragma HLS unroll factor=8
    DTYPE c = W_real[j];
    DTYPE s = W_imag[j];
    // Compute butterflies that use same W**k
    int i = j;
    int i_lower = i + numBF; // index of lower point in butterfly
    // i: 0, 1, 2, ...
    // i_lower: 512, 513, ...
    DTYPE xr_lower = X_R[i_lower];
    DTYPE xi_lower = X_I[i_lower];
    DTYPE temp_R = xr_lower * c - xi_lower * s;
    DTYPE temp_I = xi_lower * c + xr_lower * s;
    DTYPE xr = X_R[i];
    DTYPE xi = X_I[i];
    OUT_R[i_lower] = xr - temp_R;
    OUT_I[i_lower] = xi - temp_I;
    OUT_R[i] = xr + temp_R;
    OUT_I[i] = xi + temp_I;
  }
}

通过上述方式，可以将中间部分stage的操作降至512/8这个级别的循环次数，但会存在以下的问题：

  1. 部分stage的II不为1：因为cyclic划分没有办法保证前后输入输出都没有内存访问冲突，且划分的factor不能太大，实测到16已经是极限了
  2. bit_reverse是整个算法的bottleneck（这是之前我们一直没有想到的），由于访问内存地址近乎乱序，因此无论怎么划分数组（HLS只能cyclic或block划分，complete划分会超时），该函数所需时间都只能在1024这个级别

基础优化-定点数

由于是硬件实现，一个很重要的优化点是量化(quantization)。官方所给的数据类型是float，涉及大量的浮点乘加运算对FPGA来说并不友好，会存在大量的latency，因此一个直接的想法是将浮点数换成定点数。但换成定点数一个核心的问题是怎么保持精度/准确率不下降。

注意到cos和sin常数表都为6位小数精度，换成定点数后要保持原有精度不变，则需求解最小的$m$使得$2^{-m}<10^{-6}$，可以求得$m=20$，即至少需要20位定点小数才能维持原有精度。

通过实验可以得到下面数据类型，20位小数位+22位整数位可以确保结果没有太大偏差。（事实上具体需要多少位表示是一个数值计算的问题，其中的加减乘操作都会影响精度，不同stage也可以设置不同的精度大小，但这里为了方便就只是粗略设置了统一精度。）

#include <ap_fixed.h>
#include <ap_int.h>
typedef ap_fixed<42, 22> DTYPE2; // <all, int>
typedef ap_fixed<22, 2> DTYPE3;
typedef ap_uint<11> UINT;

相应的计算流程需要做显式的数据类型转换。

void bit_reverse(DTYPE X_R[SIZE], DTYPE X_I[SIZE], DTYPE2 OUT_R[SIZE], DTYPE2 OUT_I[SIZE]) {
  #pragma HLS DEPENDENCE variable=OUT_I intra WAW false
  #pragma HLS DEPENDENCE variable=OUT_R intra WAW false
  for (UINT i = 0; i < SIZE; i++) {
  #pragma HLS pipeline
      UINT reversed = reverse_bits(i); // Find the bit reversed index
    if (i < reversed) {
      // Swap the real values
      OUT_R[i] = (DTYPE2)X_R[reversed];
      OUT_R[reversed] = (DTYPE2)X_R[i];

      // Swap the imaginary values
      OUT_I[i] = (DTYPE2)X_I[reversed];
      OUT_I[reversed] = (DTYPE2)X_I[i];
    } else if (i == reversed) {
      // Swap the real values
      OUT_R[i] = (DTYPE2)X_R[reversed];

      // Swap the imaginary values
      OUT_I[i] = (DTYPE2)X_I[reversed];
    }
  }
}

template<int stage>
void fft_stages(DTYPE2 X_R[SIZE], DTYPE2 X_I[SIZE], DTYPE2 OUT_R[SIZE], DTYPE2 OUT_I[SIZE]) {
//Insert your code here
  // stage 2-9
  const int DFTpts = 1 << stage;    // DFT = 2^stage = points in sub DFT
  // 4-512
  const int numBF = DFTpts / 2;     // Butterfly WIDTHS in sub-DFT
  const int loop_times = SIZE / DFTpts;
  // 2-256
  // Perform butterflies for j-th stage
  // Compute butterflies that use same W**k
  // i and i_lower in all the loops are never the same,
  // covering 0-1024 all the elements when enumerating j
  #pragma HLS DEPENDENCE variable=OUT_I intra WAW false
  #pragma HLS DEPENDENCE variable=OUT_R intra WAW false
  dft_loop:
  for (int i_tmp = 0; i_tmp < loop_times; ++i_tmp) {
    butterfly_loop:
    for (int j = 0; j < numBF; j++) {
    #pragma HLS unroll factor=16
      DTYPE3 c = (DTYPE3)W_real[j << (10 - stage)];
      DTYPE3 s = (DTYPE3)W_imag[j << (10 - stage)];
      int i = i_tmp * DFTpts + j;
      int i_lower = i + numBF; // index of lower point in butterfly
      DTYPE2 xr_lower = (DTYPE2)X_R[i_lower];
      DTYPE2 xi_lower = (DTYPE2)X_I[i_lower];
      DTYPE2 temp_R = xr_lower * c - xi_lower * s;
      DTYPE2 temp_I = xi_lower * c + xr_lower * s;
      DTYPE2 xr = X_R[i];
      DTYPE2 xi = X_I[i];
      OUT_R[i_lower] = xr - temp_R;
      OUT_I[i_lower] = xi - temp_I;
      OUT_R[i] = xr + temp_R;
      OUT_I[i] = xi + temp_I;
    }
  }
}

另外为了减少内存访问冲突，这里采用了RAM_T2P的内存实现方式，即双端口BRAM，每个端口都可以用来读或写。

DTYPE2 Stage1_R[SIZE], Stage1_I[SIZE];
#pragma HLS bind_storage variable=Stage1_R type=RAM_T2P impl=bram latency=1
#pragma HLS bind_storage variable=Stage1_I type=RAM_T2P impl=bram latency=1
#pragma HLS array_partition variable=Stage1_R cyclic factor=16 dim=1
#pragma HLS array_partition variable=Stage1_I cyclic factor=16 dim=1

进阶优化-Stockham FFT

上面的方法已经将latency从8k压至2k以内，但是我们的排名却连前15都进不了，这非常让人不解和疑惑，因为我们难以想象基础的FFT居然还有这么大的优化空间。

一开始我们尝试寻找文献优化位反转的性能，但找到的资料寥寥无几，大多数资料都是在优化后面各个stage蝶形计算的步骤，另有少部分资料优化位反转本身（怎么由abcd快速转到dcba，但这在FPGA上是几乎不用耗时的），没有文献涉及到如何快速交换位反转后的数组元素。后来才发现，我们被主办方带进了一个死胡同，其实位反转这步操作并不是必须的，在FFT的不同实现中确实有些实现是不需要位反转的。当硬件性能无法提升时就要考虑算法是否能够再改进了，这也是非常标准的algorithm-hardware co-design的流程。

进而我们找到了所谓的Stockham FFT，这是在GPU FFT实现中非常常用的技术，它不需要进行位反转操作，而可以直接对原来数组的元素进行FFT计算，只是输入和输出的下标需要重新进行计算。

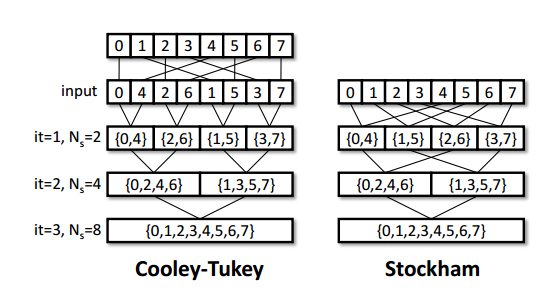
这其实跟Cooley-Tukey也类似，一开始分成4组(0,4),(1,5),(2,6),(3,7)再进行奇偶分组[(0,4),(2,6)],[(1,5),(3,7)]，对应组再进行蝶形计算。

下面是核心的代码，可以看到实现流程比Cooley-Tukey还短，只有一层循环。

template<typename in_type, typename out_type, int stage>
void fft_stages(in_type X_R[SIZE], in_type X_I[SIZE], out_type OUT_R[SIZE], out_type OUT_I[SIZE]) {
  const int half = SIZE / 2;
  const int p = 1 << (stage-1); // [1,2,4,8,...]】
  #pragma HLS DEPENDENCE variable=OUT_I intra WAW false
  #pragma HLS DEPENDENCE variable=OUT_R intra WAW false
  dft_loop:
  for (int l_in = 0; l_in < half; ++l_in) {
  #pragma HLS unroll factor=16
  #pragma HLS pipeline
    int r_in = l_in + half;
    int k = l_in % p; // 0, 1
    int l_out = ((l_in - k) << 1) + k;
    int r_out = ((l_in - k) << 1) + k + p;
    // 0, 1, 4, 5
    // 2, 3, 6, 7
    int theta = (k << 9) / p;
    DTYPE3 c = (DTYPE3)W_real[theta];//cos(-(float)k/p*PI);
    DTYPE3 s = (DTYPE3)W_imag[theta];//sin(-(float)k/p*PI);
    DTYPE2 xr_r = (DTYPE2)X_R[r_in];
    DTYPE2 xi_r = (DTYPE2)X_I[r_in];
    DTYPE2 temp_R = xr_r * c - xi_r * s;
    DTYPE2 temp_I = xi_r * c + xr_r * s;
    DTYPE2 xr = X_R[l_in];
    DTYPE2 xi = X_I[l_in];
    OUT_R[l_out] = (out_type)(xr + temp_R);
    OUT_I[l_out] = (out_type)(xi + temp_I);
    OUT_R[r_out] = (out_type)(xr - temp_R);
    OUT_I[r_out] = (out_type)(xi - temp_I);
  }
}

由于循环变规整了，因此所有stage都可以直接按照unroll 16进行展开，以提升并行度。（具体的内存访问模式最好是将每个循环中涉及到的数组下标都打印出来观察，从而确定最优的展开模式及数组划分。）同时将所有数组按cyclic factor=16循环划分，这样即可做到前面5个stage的II均为1。

对于后面5个stage，由于单一循环所做的操作有点多，故我们可以学习Cooley-Tukey拆成两个循环再进行优化，这样后面5个stage的II也可以做到1（按照上面的方法是2，这里还没搞清楚原因，不知道是不是因为l_in作为循环变量的缘故）。

template<typename in_type, typename out_type, int stage>
void fft_stages_back(in_type X_R[SIZE], in_type X_I[SIZE], out_type OUT_R[SIZE], out_type OUT_I[SIZE]) {
  const int half = SIZE / 2;
  const int p = 1 << (stage-1);
  const int out_bound = half / p;
  // stage 6: 16*32 -> 16*2
  // stage 7: 8*64 -> 8*4
  // stage 8: 4*128 -> 4*8
  // stage 9: 2*256 -> 2*16
  // stage 10: 1*512 -> 1*32
  #pragma HLS DEPENDENCE variable=OUT_I intra WAW false
  #pragma HLS DEPENDENCE variable=OUT_R intra WAW false
  out_loop:
  for (int i = 0; i < out_bound; ++i) {
    in_loop:
    for (int j = 0; j < p; ++j) {
    #pragma HLS unroll factor=16
    #pragma HLS pipeline
      int l_in = i * p + j;
      int r_in = l_in + half;
      int k = l_in % p; // 0, 1
      int l_out = ((l_in - k) << 1) + k;
      int r_out = ((l_in - k) << 1) + k + p;
      int theta = (k << 9) / p;
      DTYPE3 c = (DTYPE3)W_real[theta];//cos(-(float)k/p*PI);
      DTYPE3 s = (DTYPE3)W_imag[theta];//sin(-(float)k/p*PI);
      DTYPE2 xr_r = (DTYPE2)X_R[r_in];
      DTYPE2 xi_r = (DTYPE2)X_I[r_in];
      DTYPE2 temp_R = xr_r * c - xi_r * s;
      DTYPE2 temp_I = xi_r * c + xr_r * s;
      DTYPE2 xr = X_R[l_in];
      DTYPE2 xi = X_I[l_in];
      OUT_R[l_out] = (out_type)(xr + temp_R);
      OUT_I[l_out] = (out_type)(xi + temp_I);
      OUT_R[r_out] = (out_type)(xr - temp_R);
      OUT_I[r_out] = (out_type)(xi - temp_I);
    }
  }
}

最终10个stage均做到了II=1，并且每层循环大约只需6个时钟即可完成，故总性能为

latency=10*(512/16-1)+6=370

比原来2k又提升了5倍多的性能。

Radix-N FFT

即便是压到几百的latency，我们的排名也还进不了前十，因此应该还有更多优化空间。还是之前说的，如果硬件优化已经提升不了了，那就得考虑算法层面的提升了。

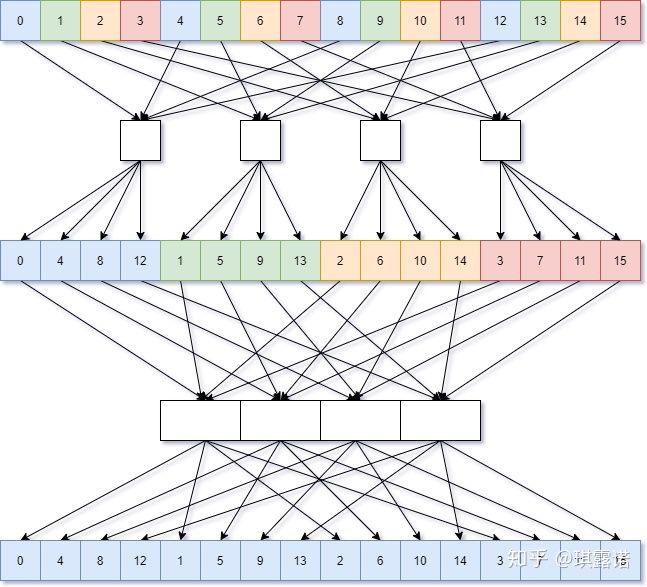
现在的问题是单一stage的性能已经很好了，但是所需stage的数目比较多（10个stage），因此我们考虑能不能用更少的stage达成一样的效果。事实上，是可以的。前面我们都是按照奇偶分拆，也即划分为2组，因此需要$\log_2 N$次蝶形计算。那如果划分的组数更多，所需要的stage数目也会呈指数级减少，这也就是以不同基数(radix)为底的FFT的思想。

划分成两组则是Radix-2，划分为四组则是Radix-4，需要进行$\log_4 N$轮迭代。（图片来源：Unity中的FFT的优化以及性能测试 - 露米 Lumi的文章 - 知乎）

\[\begin{aligned} F(k) &= F_0(k) + \overline{\omega_N^k}F_1(k) + \overline{\omega_N^{2k}}F_2(k) + \overline{\omega_N^{3k}}F_3(k)\\ F(k+N/4) &= \overline{\omega_4^1}F_0(k) + \overline{\omega_4^1}\overline{\omega_N^k}F_1(k) + \overline{\omega_4^1}\overline{\omega_N^{2k}}F_2(k) + \overline{\omega_4^1}\overline{\omega_N^{3k}}F_3(k)\\ F(k+N/2) &= \overline{\omega_4^2}F_0(k) + \overline{\omega_4^2}\overline{\omega_N^k}F_1(k) + \overline{\omega_4^2}\overline{\omega_N^{2k}}F_2(k) + \overline{\omega_4^2}\overline{\omega_N^{3k}}F_3(k)\\ F(k+3N/4) &= \overline{\omega_4^3}F_0(k) + \overline{\omega_4^3}\overline{\omega_N^k}F_1(k) + \overline{\omega_4^3}\overline{\omega_N^{2k}}F_2(k) + \overline{\omega_4^3}\overline{\omega_N^{3k}}F_3(k) \end{aligned}\]

下面代码并没有贴出全部函数，只贴了核心的fft_stages_r4函数，其他都可以由这个函数的计算过程导出。注意到这里同样为后半stage创建了fft_stages_back_r4，这里一开始是混合了Radix-2的fft_stages_back_r2，后来发现没有必要，对于Radix-4同样可以拆成两个循环后将II变为1。另外，这里为了方便更大radix代码的编写，创建了一个复数类Complex用于存储实部和虚部，HLS还是可以对这种简单的数据结构进行处理的，类函数也都会被inline。数组划分时直接指定实例名，HLS会自动将类里的元素依次划分。

template<typename T>
struct Complex {
  T r;
  T i;
  Complex() {}
  Complex(T in_r, T in_i) {
    r = in_r;
    i = in_i;
  }
  Complex<T> operator+(const Complex<T>& b) {
    return Complex<T>(this->r + b.r, this->i + b.i);
  }
  Complex<T> operator-(const Complex<T>& b) {
    return Complex<T>(this->r - b.r, this->i - b.i);
  }
  Complex<T> operator*(const Complex<DTYPE3>& b) {
    return Complex<T>(this->r * b.r - this->i * b.i, this->r * b.i + this->i * b.r);
  }
  void operator=(const Complex<T>& b) {
    this->r = b.r;
    this->i = b.i;
  }
};

inline Complex<DTYPE2> twiddle(const Complex<DTYPE2>& a) {
  return Complex<DTYPE2>(a.i, -a.r);
}

void fft(DTYPE X_R[SIZE], DTYPE X_I[SIZE], DTYPE OUT_R[SIZE], DTYPE OUT_I[SIZE])
{
#pragma HLS interface ap_ctrl_chain port=return
#pragma HLS dataflow
  #pragma HLS array_partition variable=X_R cyclic factor=16 dim=1
  #pragma HLS array_partition variable=X_I cyclic factor=16 dim=1
  #pragma HLS array_partition variable=OUT_R cyclic factor=16 dim=1
  #pragma HLS array_partition variable=OUT_I cyclic factor=16 dim=1
  Complex<DTYPE2> Stage1[SIZE];
  #pragma HLS bind_storage variable=Stage1 type=RAM_T2P impl=bram latency=1
  #pragma HLS array_partition variable=Stage1 cyclic factor=16 dim=1
  Complex<DTYPE2> Stage2[SIZE];
  #pragma HLS bind_storage variable=Stage2 type=RAM_T2P impl=bram latency=1
  #pragma HLS array_partition variable=Stage2 cyclic factor=16 dim=1
  Complex<DTYPE2> Stage3[SIZE];
  #pragma HLS bind_storage variable=Stage3 type=RAM_T2P impl=bram latency=1
  #pragma HLS array_partition variable=Stage3 cyclic factor=16 dim=1
  Complex<DTYPE2> Stage4[SIZE];
  #pragma HLS bind_storage variable=Stage4 type=RAM_T2P impl=bram latency=1
  #pragma HLS array_partition variable=Stage4 cyclic factor=16 dim=1
  Complex<DTYPE2> Stage5[SIZE];
  #pragma HLS bind_storage variable=Stage5 type=RAM_T2P impl=bram latency=1
  #pragma HLS array_partition variable=Stage5 cyclic factor=16 dim=1

  fft_stage_first_r4(X_R, X_I, Stage1); // 4
  fft_stages_r4<2>(Stage1, Stage2); // 16
  fft_stages_r4<3>(Stage2, Stage3); // 64
  fft_stages_back_r4<4>(Stage3, Stage4); // 256
  fft_stage_last_r4(Stage4, OUT_R, OUT_I); // 1024
}

template<int stage>
void fft_stages_r4(Complex<DTYPE2> X[SIZE], Complex<DTYPE2> OUT[SIZE]) {
  const int offset = SIZE >> 2; // radix 4
  const int p = 1 << ((stage - 1) * 2); // [1,4,16,64,256]
  #pragma HLS DEPENDENCE variable=OUT intra WAW false
  dft_loop:
  for (int i = 0; i < offset; ++i) {
  #pragma HLS unroll factor=16 skip_exit_check
  #pragma HLS pipeline
    int in0 = i;
    int in1 = i + offset * 1;
    int in2 = i + offset * 2;
    int in3 = i + offset * 3;
    int k = i % p;
    int out0 = ((in0 - k) << 2) + k;
    int out1 = out0 + p * 1;
    int out2 = out0 + p * 2;
    int out3 = out0 + p * 3;

    int theta = (k << 8) / p;
    Complex<DTYPE2> f0 = X[in0];
    Complex<DTYPE2> f1 = X[in1] * Complex<DTYPE3>((DTYPE3)cos_coeff[theta], (DTYPE3)sin_coeff[theta]);
    Complex<DTYPE2> f2 = X[in2] * Complex<DTYPE3>((DTYPE3)cos_coeff[theta * 2], (DTYPE3)sin_coeff[theta * 2]);
    Complex<DTYPE2> f3 = X[in3] * Complex<DTYPE3>((DTYPE3)cos_coeff[theta * 3], (DTYPE3)sin_coeff[theta * 3]);

    Complex<DTYPE2> u0 = f0 + f2;
    Complex<DTYPE2> u1 = f0 - f2;
    Complex<DTYPE2> u2 = f1 + f3;
    Complex<DTYPE2> u3 = twiddle(f1 - f3);

    OUT[out0] = u0 + u2;
    OUT[out1] = u1 + u3;
    OUT[out2] = u0 - u2;
    OUT[out3] = u1 - u3;
  }
}

Sort（中级题）

待更新…

SVM（中级题）

ECDSA（中级题）

图直径（高级题）

参考资料

  • https://github.com/sazczmh/PP4FPGAS_Study_Notes_S1C05_HLS_FFT/blob/master/fft.cpp

Related Posts